2.7 探索勾股定理(1) 同步练习（含答案）

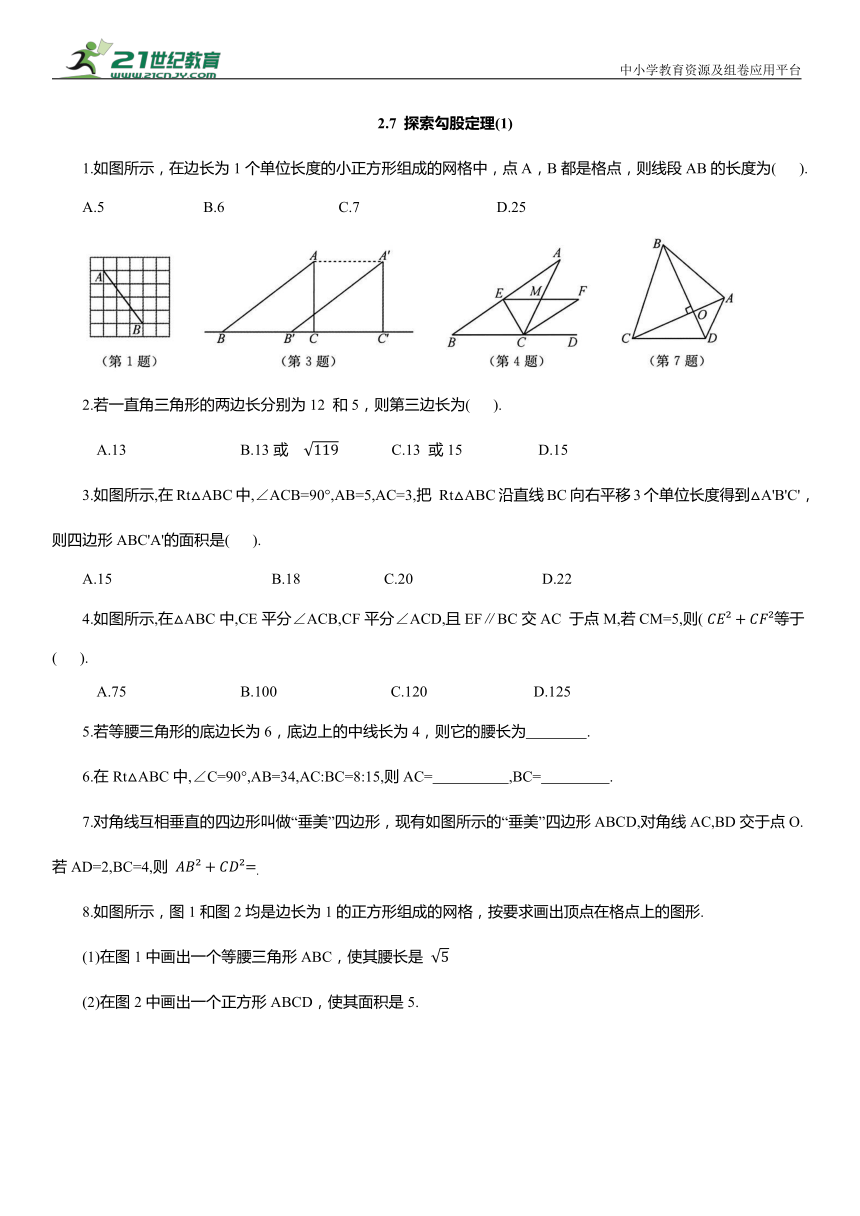
中小学教育资源及组卷应用平台 2.7 探索勾股定理(1) 1.如图所示，在边长为1个单位长度的小正方形组成的网格中，点A，B都是格点，则线段AB的长度为( ). A.5 B.6 C.7 D.25 2.若一直角三角形的两边长分别为12 和5，则第三边长为( ). A.13 B.13或 C.13 或15 D.15 3.如图所示,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,把 Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C'，则四边形ABC'A'的面积是( ). A.15 B.18 C.20 D.22 4.如图所示,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC 于点M,若CM=5,则( 等于( ). A.75 B.100 C.120 D.125 5.若等腰三角形的底边长为6，底边上的中线长为4，则它的腰长为 . 6.在Rt△ABC中,∠C=90°,AB=34,AC:BC=8:15,则AC= ,BC= . 7.对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=4,则 8.如图所示，图1和图2均是边长为1的正方形组成的网格，按要求画出顶点在格点上的图形. (1)在图1中画出一个等腰三角形ABC，使其腰长是 (2)在图2中画出一个正方形ABCD，使其面积是5. 9.如图所示,在△ABC中,AB=AC=5,AD平分∠BAC,E是AC 边的中点. (1)求 DE的长. (2)若AD的长为4,求△DEC的面积. 10.如图所示,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点 N,则MN等于( ). A. B. C. D. 11.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,分别以AB,AC,BC为边在AB的同侧作正方形ABEF，正方形ACPQ，正方形 BDMC，四块阴影部分的面积分别为 S ，S ,S ,S ,则( 等于( ). A.14 B.16 C.18 D.20 12.如图所示,在△ABC中,D是边BC上的一点,已知AC=5,AD=6,BD=10,CD=5,则△ABC的面积是 . 13.如图所示，在等腰直角三角形OAA 中， ，以OA 为直角边作等腰直角三角形OA A ，以OA 为直角边作等腰直角三角形OA A ……则OA 的长度为 14.我国古代数学家赵爽为了证明勾股定理，创制了一幅“弦图”(图1)，后人称其为“赵爽弦图”.由图1变化得到图2，它是用八个全等的直角三角形拼接而成的，记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 S , S , S . 若 则 S 的值为 15.如图所示，在四边形ABCD中， (1)求证:AB=BC. (2)当 BE⊥AD 于点E 时,试证明:BE=AE+CD. 16.阅读下列材料： 小明遇到这样一个问题：在△ABC 中，AB，BC，AC 三边的长分别为 求△ABC的面积. 小明是这样解决问题的：如图1所示，先画一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处)，借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法. 请回答： (1)图1中△ABC的面积为 . 参考小明解决问题的方法，完成下列问题： (2)图2是一个6×6的正方形网格(每个小正方形的边长为1). ①利用构图法在图2中画出三边长分别为 的格点三角形DEF. ②△DEF 的面积为 . (3)如图3所示,已知△PQR,分别以 PQ,PR 为边向外作正方形PQAF,正方形 PRDE,连结EF.若 求六边形 AQRDEF 的面积. 17.如图所示，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，若 BD 是△ABC的高,则 BD的长为( ). 18.如图1所示，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”.此图案的示意图如图2所示，其中四边形ABCD和四边形EFGH 都是正方形,△ABF,△BCG,△CDH,△DAE 是四个全等的直角三角形.若EF=2,DE=8,则AB 的长为 . 19.探索与研究： (1)如图1所示，对任意的符合条件的直角三角形，绕其锐角顶点将其旋转 90°，可知∠BAE=90°，且四边形 ACFD是一个正方形，它的面积和四边形 ABFE 的面积相等，而四边形ABFE的面积等于 Rt△BAE 和Rt△BFE的面积之和.根据图示写出证明勾股定理的过程. (2)如图2所示的图形是由任意的符合条件的两个全等的 Rt△BE ... ...