5.2菱形培优练习 浙教版2024—2025学年八年级下册（含答案）

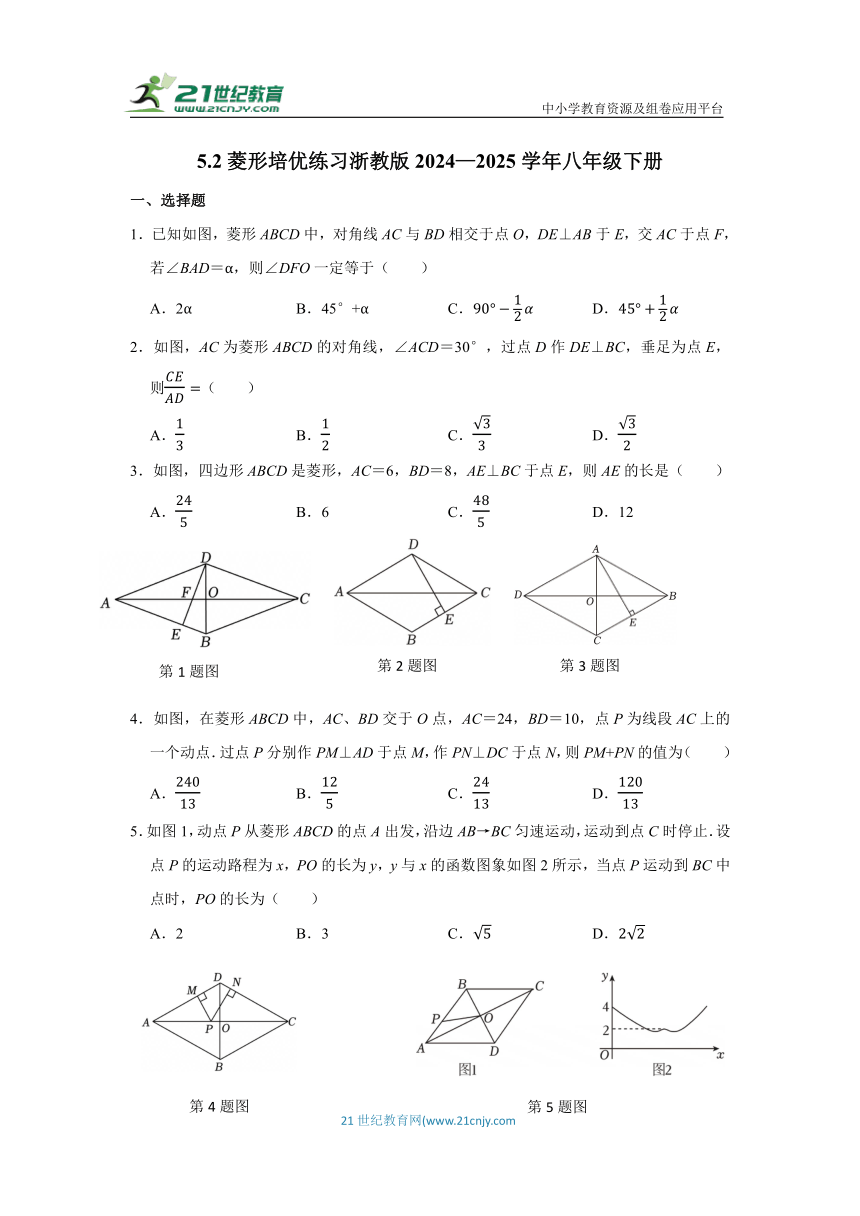
中小学教育资源及组卷应用平台 5.2菱形培优练习浙教版2024—2025学年八年级下册 一、选择题 1．已知如图，菱形ABCD中，对角线AC与BD相交于点O，DE⊥AB于E，交AC于点F，若∠BAD＝α，则∠DFO一定等于（　　） A．2α B．45°+α C． D． 2．如图，AC为菱形ABCD的对角线，∠ACD＝30°，过点D作DE⊥BC，垂足为点E，则（　　） A． B． C． D． 3．如图，四边形ABCD是菱形，AC＝6，BD＝8，AE⊥BC于点E，则AE的长是（　　） A． B．6 C． D．12 4．如图，在菱形ABCD中，AC、BD交于O点，AC＝24，BD＝10，点P为线段AC上的一个动点．过点P分别作PM⊥AD于点M，作PN⊥DC于点N，则PM+PN的值为（　　） A． B． C． D． 5．如图1，动点P从菱形ABCD的点A出发，沿边AB→BC匀速运动，运动到点C时停止．设点P的运动路程为x，PO的长为y，y与x的函数图象如图2所示，当点P运动到BC中点时，PO的长为（　　） A．2 B．3 C． D． 二、填空题 6．如图，在平行四边形ABCD中，以点A为圆心，AB为半径作弧，交AD于点F，再分别以点B，F为圆心，大于为半径作弧，两弧交于点G，射线AG交BC于点E．若BF＝8.8，AB＝5.5，则AE的长为　 　． 7．如图，菱形ABCD的对角线AC、BD相交于点O，作CE⊥AB交AB的延长线于点E，连接OE，若AB＝5，S菱形ABCD＝20，则OE＝　 　． 8．如图，在菱形ABCD中，对角线AC、BD相交于点O，点M、N分别是边AD、CD的中点，连接MN、OM．若MN＝3，S菱形ABCD＝24，则OM的长为 　 　． 9．如图，在菱形ABCD中，对角线AC、BD交于点O，AB＝10，AC＝16，点E、F分别在AB、OD上，且BE＝3，OF＝1，点P是AC上任意一点，则PE﹣PF的最大值为　 　． 三、解答题 10．如图，在四边形ABCD中，AD＝CD，BD⊥AC于点O，点E是DB延长线上一点，OE＝OD，BF⊥AE于点F． （1）求证：四边形AECD是菱形； （2）若AB平分∠EAC，OB＝3，BE＝5，求EF和AD的长． 11．如图，在 ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作 ECFG． （1）证明 ECFG是菱形； （2）若∠ABC＝120°，连接BD、CG，求∠BDG的度数； （3）若∠ABC＝90°，AB＝6，AD＝8，M是EF的中点，求DM的长． 12．已知：如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN． （1）求证：四边形BMDN是菱形； （2）若AB＝4，AD＝8，求菱形BMDN的面积． 13．如图，在 ABCD中，M、N分别是AD、BC的中点，∠AND＝90°，连接CM交DN于点O． （1）求证：△ABN≌△CDM； （2）求证：四边形CDMN为菱形； （3）过点C作CE⊥MN于点E，交DN于点P，若PE＝1，∠1＝∠2，求NC的长． 14．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE． （1）求证：∠DAC＝∠DCA； （2）求证：四边形ABCD是菱形； （3）若AB，BD＝2，求OE的长． 参考答案 一、选择题 题号 1 2 3 4 5 答案 C B A D C 1．【解答】解：∵四边形ABCD是菱形， ∴AC⊥BD，∠BAO∠BAD， ∴∠DFO+∠FDO＝90°， ∵DE⊥AB， ∴∠FDO+∠ABO＝90°， ∴∠DFO＝∠ABO， ∵∠BAO+∠ABO＝90°， ∴∠DFO＝90°﹣∠BAO＝90°， 故选：C． 2．【解答】解：由题意可知，四边形ABCD是菱形， ∴CD＝AD＝CB，且AC平分∠BCD， ∵∠ACD＝30°， ∴∠BCD＝2∠ACD＝2×30°＝60°， ∵DE⊥BC， ∴∠DEC＝90°， 在Rt△CDE中，∠CDE＝30°， ∴， 即， 故选：B． 3．【解答】解：∵四边形ABCD是菱形，AC＝6，BD＝8， ∴AC⊥BD，OC＝OAAC＝3，OB＝ODBD＝4， ∴∠BOC＝90°， ∴BC5， ∵AE⊥BC于点E， ∴S菱形ABCD＝5AE6×8， ∴AE， 故选：A． 4．【解答】解：如图，连接PD， ∵四边形ABCD是菱形， ∴AC与BD互相垂直平分， ∴AO＝OC＝12，BO＝DO＝5， ∴AD＝CD13 ... ...