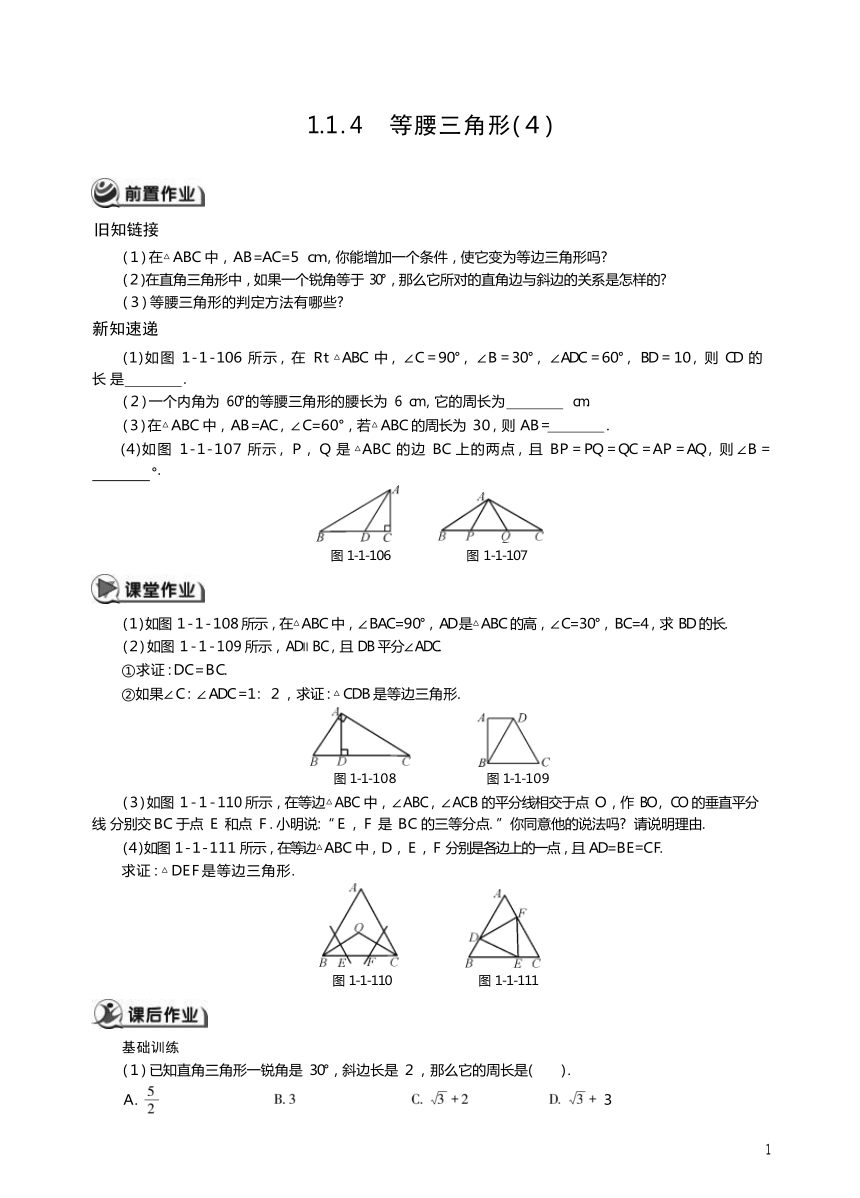
1 . 1 . 4 等腰三角形(4) 旧知链接 (1) 在△ABC 中,AB =AC=5 cm,你能增加一个条件,使它变为等边三角形吗 (2)在直角三角形中,如果一个锐角等于 30 °,那么它所对的直角边与斜边的关系是怎样的 (3) 等腰三角形的判定方法有哪些 新知速递 (1) 如 图 1-1-106 所 示, 在 Rt △ABC 中, ∠C = 90 °, ∠B = 30 °, ∠ADC = 60 °, BD = 10, 则 CD 的 长 是 . (2) 一个内角为 60°的等腰三角形的腰长为 6 cm,它的周长为 cm . (3) 在△ABC 中,AB =AC, ∠C=60 °,若△ABC 的周长为 30,则 AB = . (4) 如 图 1-1-107 所 示, P, Q 是 △ABC 的 边 BC 上 的 两 点, 且 BP = PQ = QC = AP = AQ, 则 ∠B = ° . 图 1-1-106 图 1-1-107 (1) 如图 1-1-108 所示,在△ABC 中, ∠BAC=90 °,AD 是△ABC 的高, ∠C=30 °,BC=4,求 BD 的长. 1 (2) 如图 1-1-109 所示,AD∥BC,且 DB 平分∠ADC. ①求证 :DC=BC. ②如果∠C: ∠ADC =1 : 2,求证 : △CDB 是等边三角形. 图 1-1-108 图 1-1-109 (3) 如图 1-1-110 所示,在等边△ABC 中, ∠ABC, ∠ACB 的平分线相交于点 O,作 BO, CO 的垂直平分线 分别交BC 于点 E 和点 F. 小明说:“E,F 是 BC 的三等分点. ”你同意他的说法吗 请说明理由. (4) 如图 1-1-111 所示,在等边△ABC 中,D,E,F 分别是各边上的一点,且 AD=BE=CF. 求证 : △DEF 是等边三角形. 图 1-1-110 图 1-1-111 基础训练 (1) 已知直角三角形一锐角是 30 °,斜边长是 2,那么它的周长是( ) . A . 3 (2) ①有两个角等于 60°的三角形 ②有一个角等于 60°的等腰三角形 ③三个外角( 每个顶点处各取一 个外角) 都相等的三角形 ④一腰上的中线也是这条腰上的高的等腰三角形. 以上三角形中,是等边三角形 的有( ) . 2 A . ①②③ B . ①②④ C . ①③ D . ①②③④ (3) 等边△ABC 的两条角平分线 BD 和 CE 交于点 I,则 ∠BIC 等于( ) . A . 60 ° B . 90 ° C . 120 ° D . 150 ° (4) 直角三角形中的一角为 30 °,此角的对边长是斜边长的 . (5) 如图 1-1-113 所示,在△ABC 中,AB =AC, ∠A =60 °,BE⊥AC 于 E,延长 BC 到 D,使 CD =CE,连接 DE. 若△ABC 的周长是 24,则△BDE 的周长是 . 拓展提高 (1) 如图 1-1-114 所示, △ABC 是等边三角形, 点 D 是 BC 边上任意一点,DE ⊥AB 于点 E,DF⊥AC 于点 F. 若 BC=4,则 BE +CF= . 图 1-1-114 图 1-1-113 (2) 如图 1-1-115 所示,在等边△ABC 的边 BC 上任取一点 D,作 ∠ADE =60 °,DE 交 ∠ACB 的外角平分 线于 E,则△ADE 是 三角形. (3) 在四边形 ABCD 中,AB =BC=5, ∠B =60 °,CD =7,则 AD 的取值范围是 . (4) 如图 1-1-116 所示,在△ABC 中,AB =AC, ∠BAC =120 °,AD⊥AC 交 BC 于点 D, 求证 :BC=3AD . 图 1-1-115 图 1-1-116 发散思维 (1) 如图 1-1-117 所示, △ABC 是等边三角形,分别延长 AB 至 F,延长 BC 至 D,延长 CA 至 E,使 AF = 3AB,BD =3BC,CE=3CA . 求证 : △DEF 是等边三角形. (2) 如图 1-1-118 所示, 已知点 B,C,D 在同一条直线上, △ABC 和△CDE ... ...
~~ 您好,已阅读到文档的结尾了 ~~