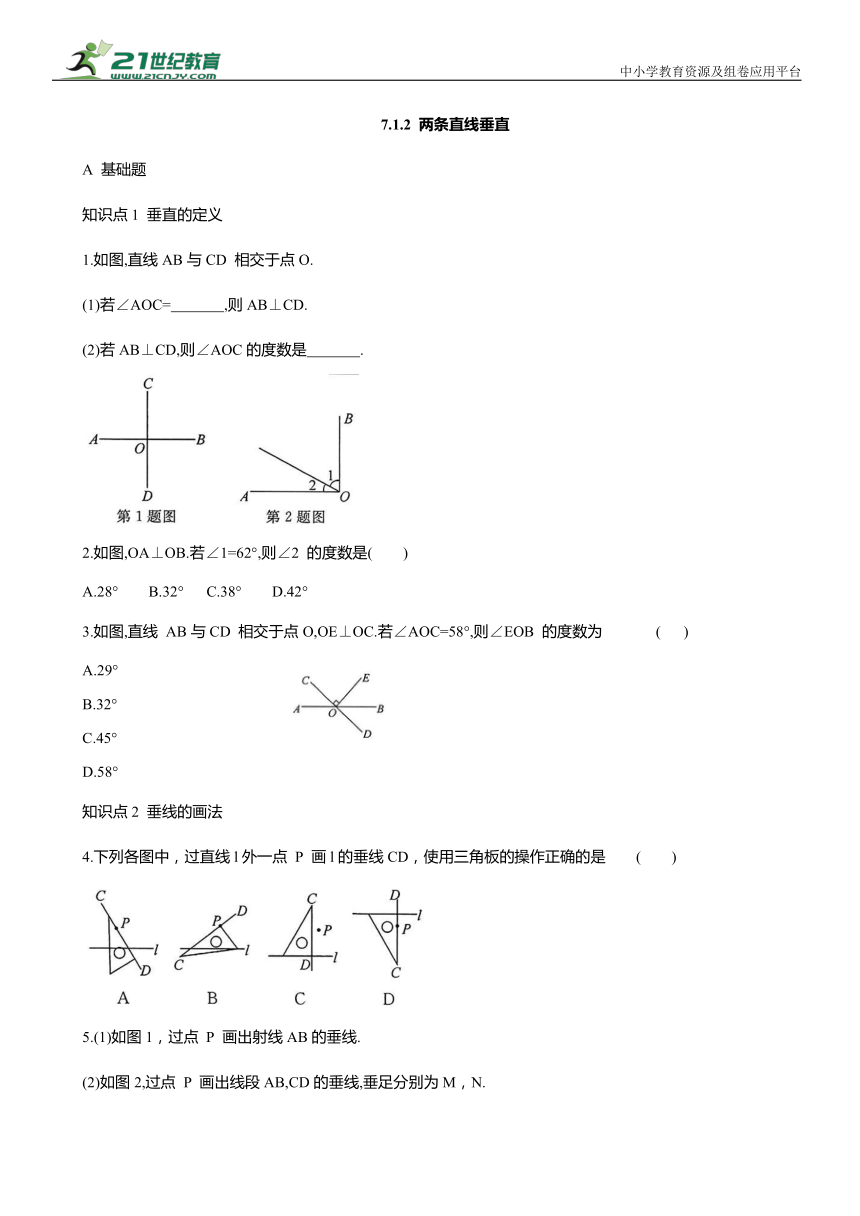
中小学教育资源及组卷应用平台 7.1.2 两条直线垂直 A 基础题 知识点1 垂直的定义 1.如图,直线AB与CD 相交于点O. (1)若∠AOC= ,则AB⊥CD. (2)若AB⊥CD,则∠AOC的度数是 . 2.如图,OA⊥OB.若∠1=62°,则∠2 的度数是( ) A.28° B.32° C.38° D.42° 3.如图,直线 AB与CD 相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB 的度数为 ( ) A.29° B.32° C.45° D.58° 知识点2 垂线的画法 4.下列各图中,过直线l外一点 P 画l的垂线CD,使用三角板的操作正确的是 ( ) 5.(1)如图1,过点 P 画出射线AB的垂线. (2)如图2,过点 P 画出线段AB,CD的垂线,垂足分别为M,N. 知识点3 关于垂线的基本事实 6.如图,在一张透明的纸上画一条直线l,在l外任取一点 Q,并折出过点 Q 且与l 垂直的直线.这样的直线能折出 条,依据是 知识点4垂线段的定义及性质 7.下列说法正确的是 ( ) A.垂线段就是与已知直线相交的线段 B.垂线段就是垂直于已知直线的线段 C.垂线段就是一条竖起来的线段 D.过直线外一点向已知直线作垂线,这一点到垂足之间的线段叫垂线段 8.如图,从直线EF 外一点 P 向EF 引四条线段PA,PB,PC,PD,其中最短的一条是 ( ) A. PA B. PB C. PC D. PD 9.自来水公司为某小区A改造供水系统.如图,沿路线 AO 铺设管道和主管道 BO 衔接(AO⊥BO),路线最短,工程造价最低,根据是 知识点5 点到直线的距离 10.下列图形中,线段 PQ的长度表示点 P 到直线a的距离的是 ( ) 11.某同学在体育课上跳远后留下的脚印如图所示,则他的跳远成绩是 ( ) A. BC 的长 B. BQ的长 C. AP 的长 D. CP 的长 易错点 未给出图形,考虑不周全致错 12.已知直线 AB,CD相交于点O,OE⊥CD,垂足为O.若∠AOE=55°,则∠BOD 的度数为 B 中档题 13.如图,已知AB⊥l,BC⊥l,垂足为B,则A,B,C三点在 上,理由是 14.如图,这是光的反射示意图,CO是入射光线,OD 是反射光线,OE 是法线,EO⊥AB,∠EOD 是反射角,∠COE=∠EOD. 若∠AOC=2∠EOD,则入 射角∠COE 的度数为 ( ) A.30° B.40° C.45° D.60° 15.如图,在直角三角形 ABC中,∠ACB=90°,BC=4 cm,AC=3cm,AB=5cm. (1)点 B 到 AC 的距离是 ;点 A 到BC 的距离是 . (2)画出表示点 C 到 AB 的距离的垂线段CD,并求出CD的长. (3)AC CD(填“>”“<”或“=”),理 由是 . 16.如图,直线 AB 与 CD 相交于点 O,OM⊥AB. (1)∠AOC 的邻补角为 (写一个即可). (2)若∠1=∠2,判断ON 与 CD 的位置关系,并说明理由. (3)若 求∠BOD 的度数. C综合题 17.如图,直线 AB,CD相交于点O,OB平分∠DOE. (1)若∠BOE:∠EOC=1:4,求∠AOC 的度数. (2)在(1)的条件下,画OF⊥CD,请直接写出∠EOF 的度数. 1.(1)90° (2)90° 2. A 3. B 4. D 5.解:(1)(2)图略. 6.1 在同一平面内,过一点有且只有一条直线与已知直线垂直 7. D 8. B 9.垂线段最短 10. C 11. C 12.145°或35° 13.同一条直线 在同一平面内,过一点有且只有一条直线与已知直线垂直 14. A 15.解:(1)4 cm 3 cm (2)图略. (3)>垂线段最短 16.解:(1)∠BOC(或∠AOD) (2)ON⊥CD.理由如下:∵OM⊥AB,∴∠AOM=∠BOM=90°.∴∠1+∠AOC=90°.∵∠1=∠2,∴∠2+∠AOC=90°,即∠CON=90°.∴ON⊥CD.(3)∵∠1= ∠BOC,∠1+∠BOM=∠BOC,∴∠BOM=3∠1.∵∠BOM= 60°. 17.解:(1)∵OB平分∠DOE,∴∠BOD=∠BOE= ∠DOE.∵∠BOE:∠EOC=1:4,∴∠EOC=4∠BOE=4∠BOD.∵∠EOC+∠DOE=180°,∴4∠BOD+2∠BOD=180°,解得∠BOD=30°.∴∠AOC=∠BOD=30°.(2)①如图1,当OF在直线AB下方时,∠EOF=30°; ②如图2,当 OF 在直线AB 上方时,∠EOF=150°.综上所述,∠EOF 的度数为30°或150°. ... ...
~~ 您好,已阅读到文档的结尾了 ~~