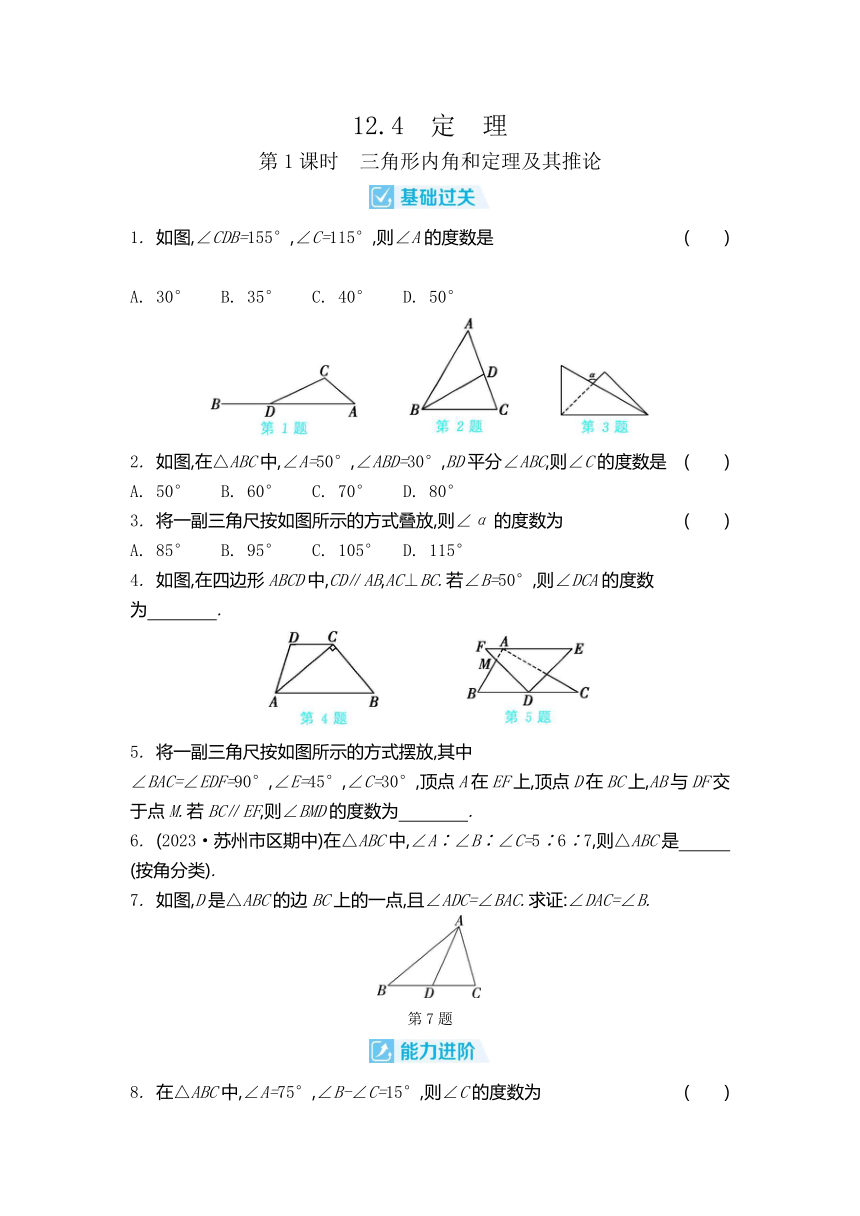
12.4 定 理 第1课时 三角形内角和定理及其推论 1. 如图,∠CDB=155°,∠C=115°,则∠A的度数是 ( ) A. 30° B. 35° C. 40° D. 50° 2. 如图,在△ABC中,∠A=50°,∠ABD=30°,BD平分∠ABC,则∠C的度数是 ( ) A. 50° B. 60° C. 70° D. 80° 3. 将一副三角尺按如图所示的方式叠放,则∠α的度数为 ( ) A. 85° B. 95° C. 105° D. 115° 4. 如图,在四边形ABCD中,CD∥AB,AC⊥BC.若∠B=50°,则∠DCA的度数为 . 5. 将一副三角尺按如图所示的方式摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,顶点A在EF上,顶点D在BC上,AB与DF交于点M.若BC∥EF,则∠BMD的度数为 . 6. (2023·苏州市区期中)在△ABC中,∠A∶∠B∶∠C=5∶6∶7,则△ABC是 (按角分类). 7. 如图,D是△ABC的边BC上的一点,且∠ADC=∠BAC.求证:∠DAC=∠B. 第7题 8. 在△ABC中,∠A=75°,∠B-∠C=15°,则∠C的度数为 ( ) A. 30° B. 45° C. 50° D. 10° 9. 如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为 ( ) A. 65° B. 70° C. 75° D. 85° 10. 如图,∠1,∠2,∠3,∠4的关系正确的是 ( ) A. ∠1+∠2=∠3+∠4 B. ∠1-∠3=∠2-∠4 C. ∠1+∠2=∠4-∠3 D. ∠1+∠3=∠2+∠4 11. 在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B的度数为 . 12. 如图,在△ABC中,AD平分∠BAC.若∠2=70°,则∠1+∠3= °. 13. 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB. (1) 若∠A=40°,则∠BOC的度数为 ; (2) 求证:∠BOC=90°+∠A. 第13题 14. 如图,在△ABC中,AD是△ABC的高,AE平分∠BAC,∠C>∠B. (1) 若∠B=30°,∠C=50°,则∠DAE的度数为 ; (2) 试猜想∠DAE与∠C-∠B之间的数量关系,并说明理由. 第14题 第2课时 多边形的内角和、外角和定理 1. 六边形内角和的度数为 ( ) A. 180° B. 360° C. 540° D. 720° 2. 一个多边形的内角和为900°,则这个多边形是 ( ) A. 七边形 B. 八边形 C. 九边形 D. 十边形 3. (2023·苏州市区期中)若一个多边形的每一个外角都是36°,则这个多边形的边数是 ( ) A. 7 B. 8 C. 9 D. 10 4. 如图,在七边形ABCDEFG中,AB,ED的延长线相交于点O.若七边形ABCDEFG在∠1,∠2,∠3,∠4处的外角的度数之和为220°,则∠BOD的度数为 ( ) A. 40° B. 45° C. 50° D. 60° 5. n边形的内角和比(n+1)边形的内角和小 °(n为整数,且n≥3). 6. 如图,在五边形ABCDE中,∠A=45°,直线l分别与边AB,AE相交于点M,N,则∠1+∠2= °. 7. (2023·兰州)如图所示为我国古建筑墙上采用的八角形空窗的示意图,其轮廓是一个每个内角都相等的八边形,则该八角形空窗的一个外角∠1的度数为 . 8. 如图,小明从点A出发沿直线前进10m到达点B,向左转45°后又沿直线前进10m到达点C,再向左转45°后沿直线前进10m到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为 m. 9. 如图,五边形ABCDE的每个内角都相等,且AB∥EC,那么∠DEC与∠DCE相等吗 为什么 第9题 10. (2024·西藏)已知正多边形的一个外角为60°,则这个正多边形的内角和为 ( ) A. 900° B. 720° C. 540° D. 360° 11. 一个多边形切去一个角后,形成的另一个多边形的内角和为1 080°,那么原多边形的边数为 ( ) A. 7 B. 7或8 C. 8或9 D. 7或8或9 12. 如图,D,E,F分别是△ABC的边BC,AC,AB上的点,则∠1+∠2+∠3+∠4+∠5+∠6 的度数是 ( ) A. 180° B. 240° C. 360° D. 540° 13. (1) 已知一个多边形的内角和与外角和的差是1 260°,则这个多边形是 边形; (2) (2023·常 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

