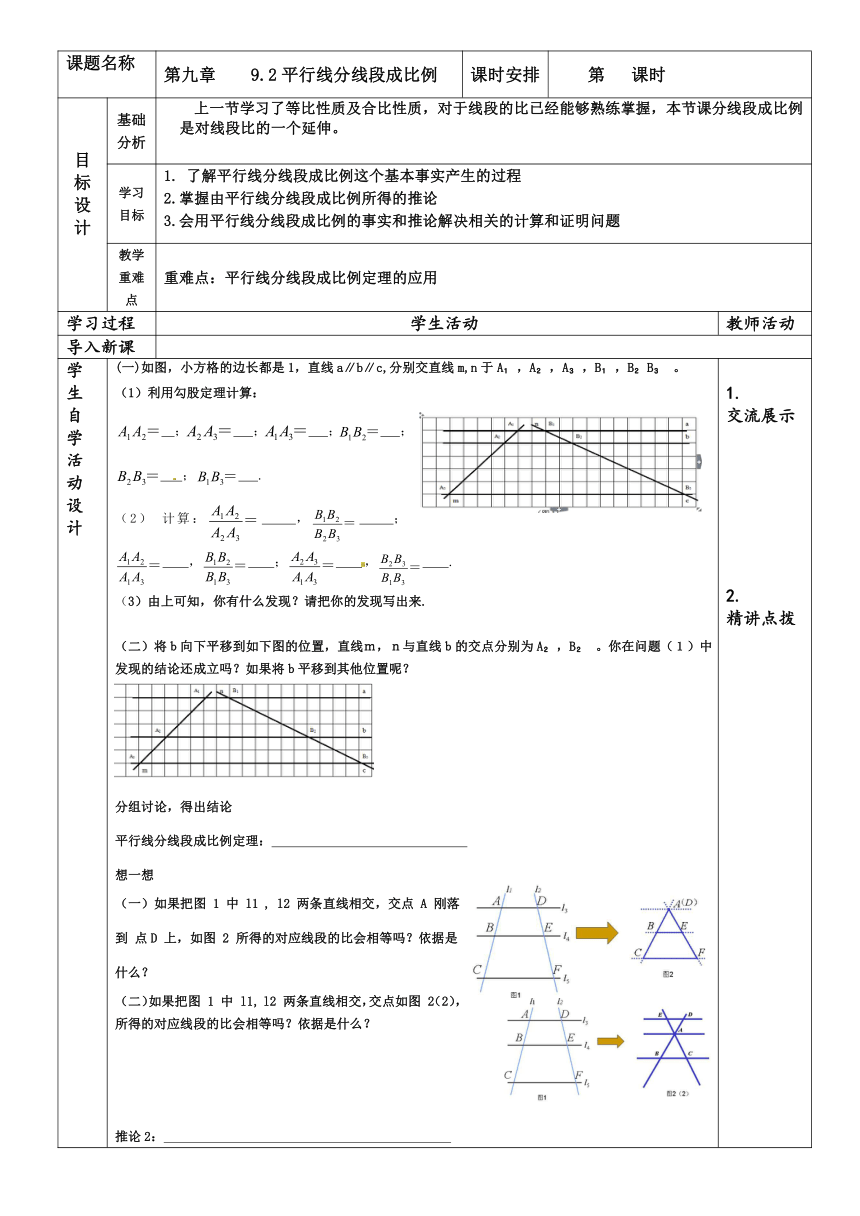
课题名称 第九章 9.2平行线分线段成比例 课时安排 第 课时 目 标 设 计 基础分析 上一节学习了等比性质及合比性质,对于线段的比已经能够熟练掌握,本节课分线段成比例是对线段比的一个延伸。 学习目标 了解平行线分线段成比例这个基本事实产生的过程 2.掌握由平行线分线段成比例所得的推论 3.会用平行线分线段成比例的事实和推论解决相关的计算和证明问题 教学重难点 重难点:平行线分线段成比例定理的应用 学习过程 学生活动 教师活动 导入新课 学生自学活动设计 (一)如图,小方格的边长都是1,直线a∥b∥c,分别交直线m,n于A ,A ,A ,B ,B B 。 (1)利用勾股定理计算: ; ; ; ; ; . (2) 计算: , ; , ; , . (3)由上可知,你有什么发现?请把你的发现写出来. (二)将b向下平移到如下图的位置,直线m,n与直线b的交点分别为A ,B 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢? 分组讨论,得出结论 平行线分线段成比例定理: 想一想 (一)如果把图 1 中 l1 , l2 两条直线相交,交点 A 刚落到 点D 上,如图 2 所得的对应线段的比会相等吗?依据是什么? (二)如果把图 1 中 l1, l2 两条直线相交,交点如图 2(2), 所得的对应线段的比会相等吗?依据是什么? 推论2: 1. 交流展示 2. 精讲点拨 巩 固 训 练 基础练习 1.如图,AD//BE//CE,且AB=2,BC=4,EF=6,则DE=_____. 第1题 第2题 第3题 2.如图,AB//CD,且AO=2,AC=6,BO=3,则BD=_____. 3.如图,BC//DE,若AD=2,AE=4,AB=6,则CE=_____. 拓展训练 1.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,BC=20cm,求BF的长. 2.如图(1),在三角形ABC中,M是AC的中点,E是AB上一点,且,连接EM并延长,交BC的延长线于D,则=_____. 3.如图,已知三角形ABC中,AD是BC边上的中线,E是AD 上的一点,且BE=AC,延长BE交AC于F。求证:AF=EF。 3.拓展反思 系统总结 达 标 检 测 1.如图,在△ABC中,DE∥BC,EF∥CD,那么下列结论错误的是( ) A.= B.= C.= D.= 2.如图,在平行四边形ABCD中,点E在边DC上,联结AE并延长交BC的延长线于点F,若AD=3CF,那么下列结论中正确的是( ) A.FC:FB=1:3 B.CE:CD=1:3 C.CE:AB=1:4 D.AE:AF=1:2. 板书设计 平行线分线段成比例及推论 (1)两条直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段) (2)平行于三角形一边的直线与其他两边相交,截得的对应线段成比例 教学反思
~~ 您好,已阅读到文档的结尾了 ~~