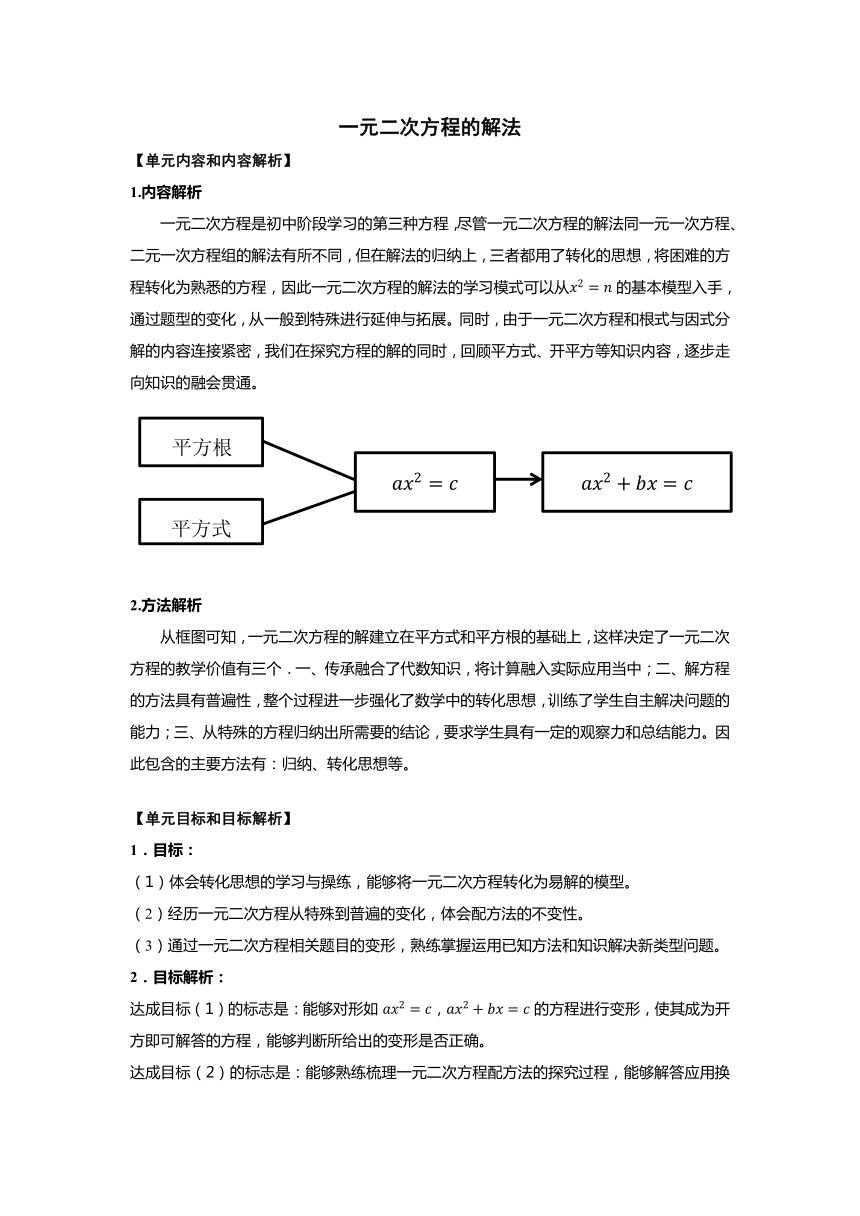
一元二次方程的解法 【单元内容和内容解析】 1.内容解析 一元二次方程是初中阶段学习的第三种方程,尽管一元二次方程的解法同一元一次方程、二元一次方程组的解法有所不同,但在解法的归纳上,三者都用了转化的思想,将困难的方程转化为熟悉的方程,因此一元二次方程的解法的学习模式可以从的基本模型入手,通过题型的变化,从一般到特殊进行延伸与拓展。同时,由于一元二次方程和根式与因式分解的内容连接紧密,我们在探究方程的解的同时,回顾平方式、开平方等知识内容,逐步走向知识的融会贯通。 2.方法解析 从框图可知,一元二次方程的解建立在平方式和平方根的基础上,这样决定了一元二次方程的教学价值有三个.一、传承融合了代数知识,将计算融入实际应用当中;二、解方程的方法具有普遍性,整个过程进一步强化了数学中的转化思想,训练了学生自主解决问题的能力;三、从特殊的方程归纳出所需要的结论,要求学生具有一定的观察力和总结能力。因此包含的主要方法有:归纳、转化思想等。 【单元目标和目标解析】 1.目标: (1)体会转化思想的学习与操练,能够将一元二次方程转化为易解的模型。 (2)经历一元二次方程从特殊到普遍的变化,体会配方法的不变性。 (3)通过一元二次方程相关题目的变形,熟练掌握运用已知方法和知识解决新类型问题。 2.目标解析: 达成目标(1)的标志是:能够对形如,的方程进行变形,使其成为开方即可解答的方程,能够判断所给出的变形是否正确。 达成目标(2)的标志是:能够熟练梳理一元二次方程配方法的探究过程,能够解答应用换元法、整体法或其他方法的题目。 达成目标(3)的标志是:熟练解出一元二次方程,能够依据现有知识进行拓展,解决其他类型的问题;对转化思想有清晰的认知,熟练运用该方法解决新的问题。 【单元教学问题诊断分析】 具备的基础(知识、能力) 学生在七年级已经学习了代数式和平方根的相关知识,熟悉代数式的运算与平方式的特征,还学习了完全平方公式和平方差公式,对代数式的判断有一定的知识基础和研究经验。 与本课目标的差距分析(知识、能力) 学生过往学习的知识是独立的,碎片化的,而在一元二次方程的解法中要求学生串联知识,并根据不同的方程的实际情况进行判断和调整,如何将陌生的方程转化为熟悉的等式,如何归纳繁多的种类,是我们目标达成的重要环节。 可能存在的问题(问题、障碍) 学生可能已经先行地学习过一元二次方程解法的公式而忽略了公式得出的过程,从而忽略了数学学习中转化思想的重要性,缺少了体验环节;也可能由于前序知识的不扎实,导致在融合应用的过程中出现基础性错误,导致推导一元二次方程的解的过程中体验的不连贯性。 应对策略(过程、方法) 避免提出如何解方程的问题,从细节入手询问学生的思考方式与角度;在提问上避免常规问题,反其道而行,要求学生展示计算过程与细节。深入体会转化过程,使学生从中体会到数学的美妙,达到沉浸式学习的目的。 对于单元整体来说,存在的障碍主要有以下几点:1.分类后不同一元二次方程解决办法的归纳总结;2.转化思想的应用。 基于以上分析,确定本单元的教学难点: 基础知识回顾的全面进行 从特殊到普遍的归纳 不同问题中的不变性 具体问题的综合应用 【单元教学过程设计】 一元二次方程的解法 (1)复习回顾 问题:在过去的学习中,我们接触了许多与平方、立方根相关的知识,同学们能不能帮助老师一起回忆一下这些知识点呢? 师生活动:学生会从较多的方面提到相关知识,包括平方、平方根的计算,平方式的特点等,从中筛选出有利于课堂的知识,引导学生将注意点落在平方式和平方根的计算上,对平方式的特点和平方根的两种情况做强调,帮助学生回忆相关知识点。 【设计意图】回 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

