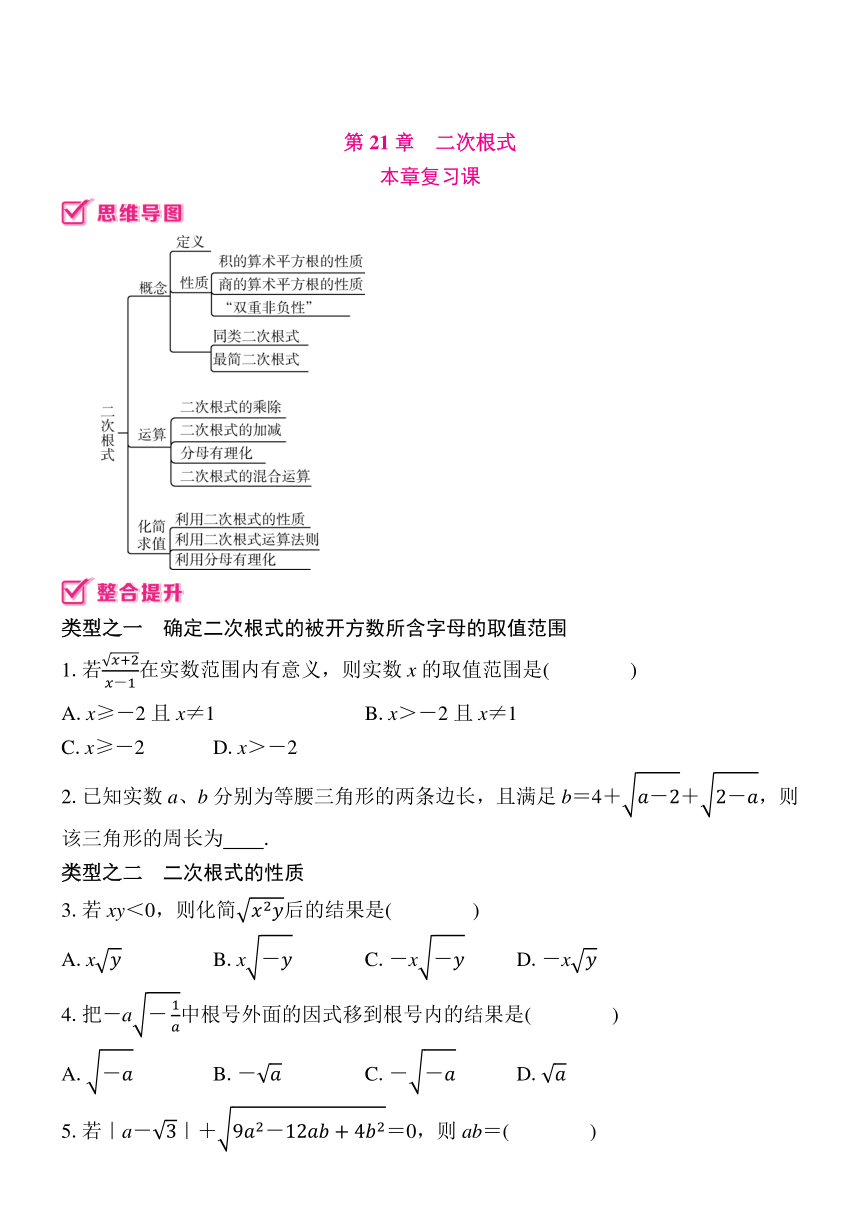
第21章 二次根式 本章复习课 类型之一 确定二次根式的被开方数所含字母的取值范围 1.若在实数范围内有意义,则实数x的取值范围是( ) A.x≥-2且x≠1 B.x>-2且x≠1 C.x≥-2 D.x>-2 2.已知实数a、b分别为等腰三角形的两条边长,且满足b=4++,则该三角形的周长为 . 类型之二 二次根式的性质 3.若xy<0,则化简后的结果是( ) A.x B.x C.-x D.-x 4.把-a中根号外面的因式移到根号内的结果是( ) A. B.- C.- D. 5.若|a-|+=0,则ab=( ) A. B. C.4 D.9 6.[2024春·长沙县期中]已知实数a、b、c在数轴上对应点的位置如图所示,化简: |a|-+-= . 7.若为整数,x为正整数,则x的值可能为 . 类型之三 二次根式的运算 8.[2024·重庆B卷]估计×(+)的值应在( ) A.8和9之间 B.9和10之间 C.10和11之间 D.11和12之间 9.计算: (1)2×(1-)+; (2)(4+3)÷2; (3)-2+-3; (4)(3-2)(3+2). 10.解答下列问题. (1)化简:= ,= ; (2)比较-和-的大小; (3)计算:(+++…+)(+1). 类型之四 二次根式的化简求值 11.[2024·眉山期末]已知x=2-,y=2+. (1)求x+y和xy的值; (2)求x2+y2-3xy的值; (3)若x的小数部分是a,y的整数部分是b,求ax-by的值. 12.规定(a,b)表示一对数对,给出如下定义:m=,n= (a>0,b>0).将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.例如,数对(4,1)的一对“对称数对”为与. (1)数对(4,3)的一对“对称数对”是 . (2)若数对(2,y)的一对“对称数对”相同,则y的值是多少? (3)若数对(a,b)的一个“对称数对”是(,3),求a、b的值. 类型之五 二次根式的实际应用 13.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边a、b、c,求面积的公式,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把以上这段文字写成公式,即为S=.现有周长为18的三角形的三边满足a∶b∶c=4∶3∶2,则用以上给出的公式求得这个三角形的面积为 . 14.[2024秋·杏花岭区月考]将边长分别为1、1+、1+2、1+3的正方形的面积记为S1、S2、S3、S4. (1)计算:S2-S1、S3-S2、S4-S3. (2)把边长为1+(n-1)的正方形的面积记作Sn,其中n是正整数,根据(1)中计算的结果,你能猜出Sn+1-Sn等于多少吗?并说明理由. (3)若将边长变为a、a+、a+2、a+3时,则Sn+1-Sn的值是多少? 综合与实践:探究两个正数之和与这两个正数之积的算术平方根的两倍之间的关系. 【探究发现】 6+6=2=12; +=2=; 0.3+0.3=2=0.6; +3>2=2; 0.2+3.2>2=1.6; +>2=. 【猜想结论】 若a>0,b>0,则有a+b≥2(当且仅当a=b时,等号成立). 【证明结论】 ∵(-)2≥0, ∴①当且仅当-=0,即a=b时,a-2+b=0,即a+b=2; ②当-≠0,即a≠b时,a-2+b>0,即a+b>2. 综合上述,若a>0,b>0,则有a+b≥2(当且仅当a=b时,等号成立). 【应用结论】 (1)对于函数y=x+(x>0),当x取何值时,y的值最小?最小值是多少? (2)对于函数y=+x(x>5),当x取何值时,y的值最小?最小值是多少? 【拓展应用】 (3)如图,学校计划一边靠墙,其余边用篱笆围成三小块面积均为24m2的矩形苗圃,中间用两道篱笆隔断.设每小块苗圃垂直于墙的一边长为xm,当x为何值时,所用篱笆的总长度最短?最短长度是多少? ... ...
~~ 您好,已阅读到文档的结尾了 ~~

