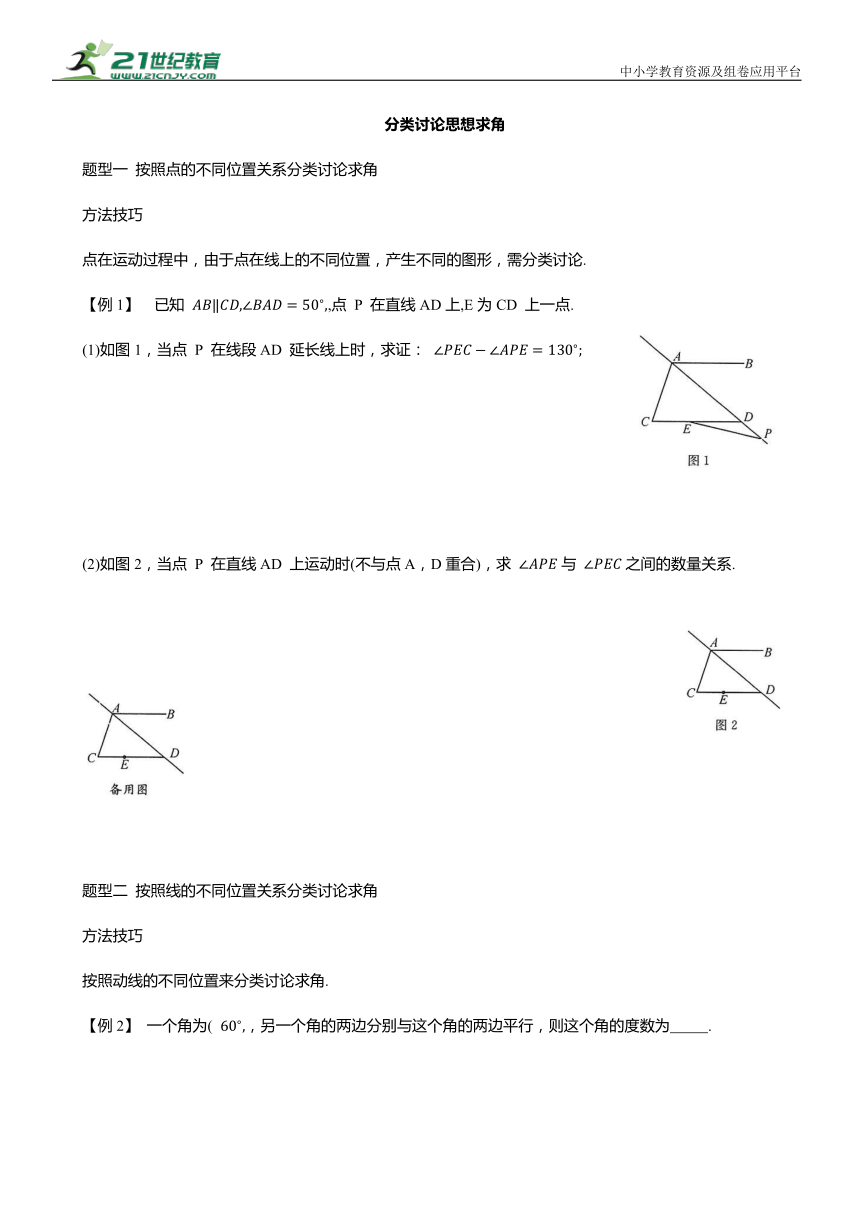
中小学教育资源及组卷应用平台 分类讨论思想求角 题型一 按照点的不同位置关系分类讨论求角 方法技巧 点在运动过程中,由于点在线上的不同位置,产生不同的图形,需分类讨论. 【例1】 已知 ,点 P 在直线AD上,E为CD 上一点. (1)如图1,当点 P 在线段AD 延长线上时,求证: (2)如图2,当点 P 在直线AD 上运动时(不与点A,D重合),求 与 之间的数量关系. 题型二 按照线的不同位置关系分类讨论求角 方法技巧 按照动线的不同位置来分类讨论求角. 【例2】 一个角为( ,另一个角的两边分别与这个角的两边平行,则这个角的度数为 . 题型三 分类讨论求角之间的关系 方法技巧 点在运动时,两个动角之间具有某种确定的数量关系,此时设未知数,探求它们之间的关系. 【例3】 如图,已知 ,BE平分 DE平分 求证: (2)H是直线CD上一动点(不与点D重合),BI平分∠HBD交CD 于点I,在图2或备用图中,请你画出图形,并猜想∠EBI 与∠BHD的数量关系,且说明理由. 针对练习8 1.如果两个角的两边分别平行,且一个角比另一个角的两倍少30°,则这两个角的度数分别是 2.如图,AB∥CD,直线 EF与直线AB,CD分别交于点E,F,∠BEF<150°,点P 为直线EF 左侧平面上一点,且∠BEP=150°,∠EPF=50°,则∠DFP 的度数是 3.(1)如图1,F是OC 边上一点,求证:∠AFC=∠AOC+∠OAF; (2)如图2,∠AOB=40°,OC平分∠AOB,点D,E在射线OA,OC上,点P 是射线OB 上的一个动点,连接DP交射线OC于点F,设∠ODP=x°.若DE⊥OA,是否存在这样的x的值,使得∠EFD=4∠EDF 若存在,求出x的值;若不存在,说明理由. 分类讨论思想求角 题型一 按照点的不同位置关系分类讨论求角 方法技巧 点在运动过程中,由于点在线上的不同位置,产生不同的图形,需分类讨论. 【例1】 已知AB∥CD,∠BAD=50°,点 P 在直线AD上,E为CD上一点. (1)如图1,当点 P 在线段AD 延长线上时,求证:∠PEC-∠APE=130°; 【分析】 按照平行线+拐点基本图形方法处理. 【解答】 过点 P作PF∥AB.∵AB∥CD,∴PF∥AB∥CD. ∴∠APF=∠BAD=50°.设∠APE=x,则∠EPF=50°-x, ∠PEC=180°-∠EPF=180°-(50°-x)=130°+x, ∴∠PEC-∠APE=130°+x-x=130°. (2)如图2,当点 P在直线AD 上运动时(不与点 A,D重合),求∠APE与∠PEC之间的数量关系. 【解答】 ①当点 P在线段AD上时,作PF∥AB, 易得PF∥AB∥CD.设∠APE=x,则∠EPF=x-50°, ∠PEC=180°-∠EPF=180°-(x-50°)=230°-x, ∴∠PEC+∠APE=230°-x+x=230°; ②当点 P 在线段DA 延长线上时,作PF∥AB, 易得PF∥AB∥CD,∠APF=∠BAD=50°,设∠APE=x, 则∠FPE=∠PEC=∠APF+∠APE=50°+x, ∴∠PEC-∠APE=50°+x-x=50°. 题型二 按照线的不同位置关系分类讨论求角 方法技巧 按照动线的不同位置来分类讨论求角. 【例2】 一个角为60°,另一个角的两边分别与这个角的两边平行,则这个角的度数为 60°或120° . 【分析】 另一个角与60°相等或与60°角互补. 【解答】 故这个角为 60°或120°. 题型三 分类讨论求角之间的关系 方法技巧 点在运动时,两个动角之间具有某种确定的数量关系,此时设未知数,探求它们之间的关系. 【例3】 如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC. 求证:BE⊥DE; (2)H是直线CD上一动点(不与点 D重合),BI平分∠HBD交CD 于点I,在图2或备用图中,请你画出图形,并猜想∠EBI 与∠BHD的数量关系,且说明理由. 【分析】 (1)根据基本图作辅助线即可得到 BE⊥DE; (2)分点H在点D的左边和右边两种情况,表示出∠ABH和∠EBI,从而得解. 【解答】 (1)证明:过点E作EF∥AB. ∵AB∥CD,EF∥AB,∴EF∥CD,∴∠FED=∠EDC.∵EF∥AB,∴∠ABE=∠BEF, ∵AB∥CD,∴∠ABD+∠CDB=180°, ∵BE平分∠ABD,DE平分 DE; (2)∠BHD=2∠EBI或∠BHD=180°-2∠EBI. 理由:∵BE平分∠ABD,∴∠ABD=2∠EBD,∵BI平分∠HBD,∴∠ ... ...
~~ 您好,已阅读到文档的结尾了 ~~