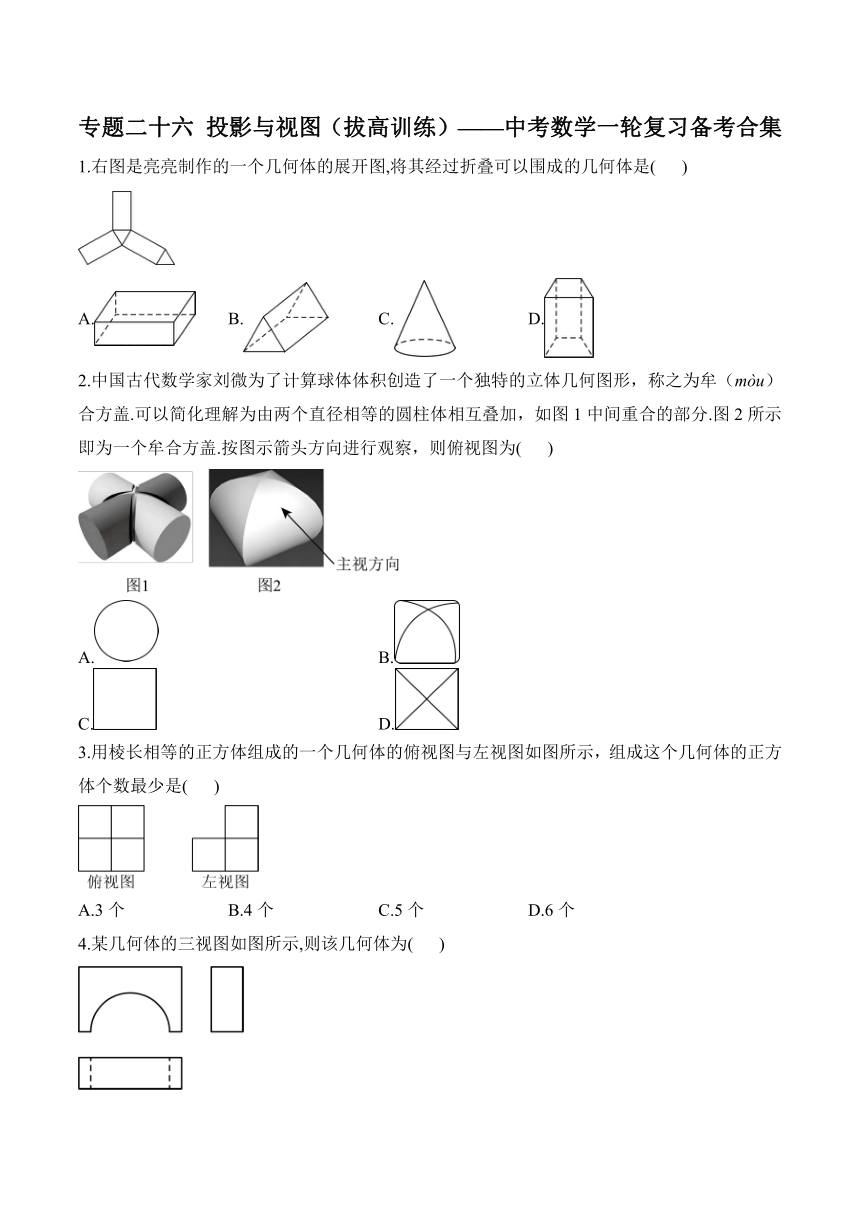
专题二十六 投影与视图 拔高训练（含答案） 2025年中考数学一轮复习

专题二十六 投影与视图（拔高训练）———中考数学一轮复习备考合集 1.右图是亮亮制作的一个几何体的展开图,将其经过折叠可以围成的几何体是( ) A. B. C. D. 2.中国古代数学家刘微为了计算球体体积创造了一个独特的立体几何图形，称之为牟（mòu）合方盖.可以简化理解为由两个直径相等的圆柱体相互叠加，如图1中间重合的部分.图2所示即为一个牟合方盖.按图示箭头方向进行观察，则俯视图为( ) A. B. C. D. 3.用棱长相等的正方体组成的一个几何体的俯视图与左视图如图所示，组成这个几何体的正方体个数最少是( ) A.3个 B.4个 C.5个 D.6个 4.某几何体的三视图如图所示,则该几何体为( ) A. B. C. D. 5.图是一个正方体的表面展开图,正方体相对两个面上的代数式的积相同则A为( ) A. B. C. D. 6.如图，小明家的客厅有一张高米的圆桌，直径为1米，在距地面2米的A处有一盏灯，圆桌的影子最外侧两点分别为D、E，依据题意建立如图所示的平面直角坐标系，其中点D的坐标为，则点E的坐标是( ) A. B. C. D. 7.如图，是一个几何体的三视图，那么这个几何体的侧面积是( ) A. B. C. D. 8.某一时刻，与地面垂直的长的木杆在地面上的影长为.同一时刻，树的影子一部分落在地面上，一部分落在坡角为的斜坡上，如图所示.已知落在地面上的影长为.落在斜坡上的影长为.根据以上条件，可求出树高为( ).（结果精确到） A. B. C. D. 9.如图,三角形硬纸板(记为)在灯光照射下形成投影,若,,则的长是_____. 10.如图，在大长方形中截取两个相同的圆作为圆柱的上下底面，剩余的小长方形作为圆柱的侧面，刚好能组合成圆柱.设大长方形的长和宽分别为y和x，则因变量y与自变量x之间的关系式为_____. 11.如图，在中，，棱长为1的立方体展开图有两边分别在，上，有两个顶点在斜边上，则的面积为_____. 12.如图，将一块含角的三角板的直角顶点C放置于直线n上，点A，点M在直线n上的正投影分别为点D，点N，若，，则在直线n上的正投影的长是_____. 13.根据三视图，求几何体的表面积，并画出这个几何体的展开图. 14.如图,电线杆上有盏路灯O,小明从点F出发,沿直线运动,当他运动2m到达点D处时(即),测得影长,再前进2m到达点B处时(即),测得影长.(图中线段、、表示小明的身高,且、、均与垂直) (1)请画出路灯O的位置和小明位于F处时,在路灯灯光下的影子； (2)求小明位于F处的影长. 答案以及解析 1.答案：B 解析：根据亮亮制作的一个几何体的展开图,可以看到底面为三角形,侧面为长方形,可以围成的几何体为三棱柱； 故选：B 2.答案：D 解析：由上向下观察物体得到的视图是， ∴它的俯视图是D选项. 故选：D. 3.答案：C 解析：由俯视图可以看出组成这个几何体的底面小正方体有4个，由左视图可知第二层最少有1个， 故组成这个几何体的小正方体的个数最少为：（个）. 故选：C. 4.答案：B 解析：由三视图可知, 该几何体为 故选：B. 5.答案：D 解析：这是一个正方体的平面展开图,共有六个面,其中面“”与面“A”相对,面“”与面“”相对, 由题意可得：, ∴ . 故选D. 6.答案：A 解析：如图所示： 由题意得：轴，， ，， ，， ， ， ， ， ， ， ， 即：， 故选：A. 7.答案：B 解析：根据题意得：这个几何体为圆锥， 如图，过点A作于点D， 根据题意得：，，， ， ， 即圆锥的母线长为5， 这个几何体的侧面积是. 故选：B 8.答案：D 解析：过点D作于点E，连接并延长，交延长线于点F， ，， ， 长的木杆在地面上的影长为， ，则， ， 长的木杆在地面上的影长为， ，则， 故选：D. 9.答案： 解析：由中心投影的定义可得与是位似三角形, ∴,且由位似得, ∴, 得：, 故答案为：. 10.答案： 解析：由题意得，圆柱的上下底面圆的半径为，圆柱的侧面展开图的长为，因为圆柱的侧面展开图的长等于底面圆的 ... ...