2025年九年级数学中考二轮复习专题复习特殊平行四边形的证明与计算（含答案）

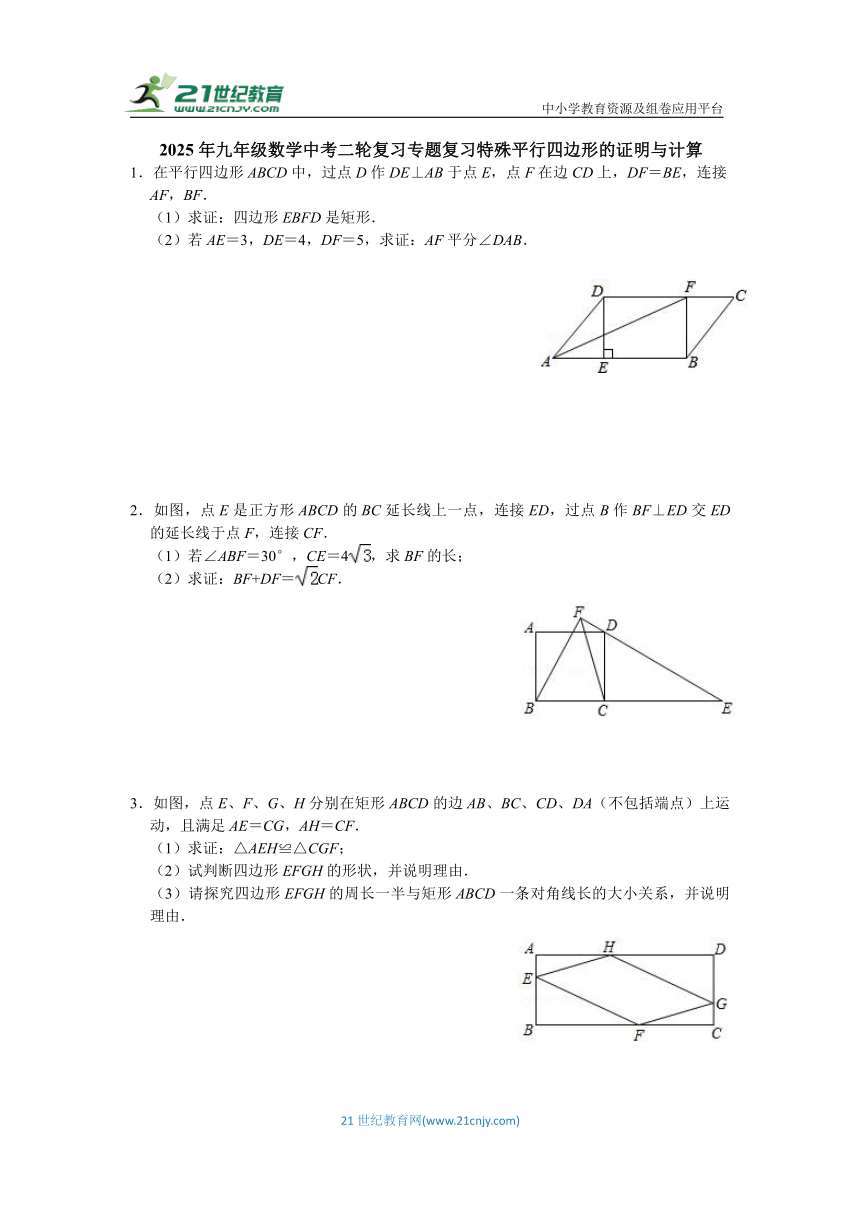
中小学教育资源及组卷应用平台 2025年九年级数学中考二轮复习专题复习特殊平行四边形的证明与计算 1．在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF． （1）求证：四边形EBFD是矩形． （2）若AE＝3，DE＝4，DF＝5，求证：AF平分∠DAB． 2．如图，点E是正方形ABCD的BC延长线上一点，连接ED，过点B作BF⊥ED交ED的延长线于点F，连接CF． （1）若∠ABF＝30°，CE＝4，求BF的长； （2）求证：BF+DF＝CF． 3．如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA（不包括端点）上运动，且满足AE＝CG，AH＝CF． （1）求证：△AEH≌△CGF； （2）试判断四边形EFGH的形状，并说明理由． （3）请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由． 4．如图，在矩形ABCD中，AB＝3，BC＝4．M、N在对角线AC上，且AM＝CN，E、F分别是AD、BC的中点． （1）求证：△ABM≌△CDN； （2）点G是对角线AC上的点，∠EGF＝90°，求AG的长． 5．如图，菱形ABCD中，作BE⊥AD、CF⊥AB，分别交AD、AB的延长线于点E、F． （1）求证：AE＝BF； （2）若点E恰好是AD的中点，AB＝2，求BD的值． 6．如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE＝DF，连结AE、AF、EF． （1）求证：△ABE≌△ADF； （2）若AE＝5，请求出EF的长． 7．如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE． （1）求证：AE＝BC； （2）若AB＝3，CD＝1，求四边形ABCE的面积． 8．如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF． （1）求证：△ABE≌△CDF； （2）当AC⊥EF时，四边形AECF是菱形吗？请说明理由． 9．如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2． （1）求平行四边形ABCD的面积； （2）求证：BD⊥BC． 10．如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE＝CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF．求证： （1）AE⊥BF； （2）四边形BEGF是平行四边形． 11．如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD中点，连接OE．过点C作CF∥BD交OE的延长线于点F，连接DF． 求证：（1）△ODE≌△FCE； （2）四边形OCFD是矩形． 12．如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q． （1）求证：△PDE≌△QCE； （2）过点E作EF∥BC交PB于点F，连结AF，当PB＝PQ时， ①求证：四边形AFEP是平行四边形； ②请判断四边形AFEP是否为菱形，并说明理由． 13．如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB、CD边于点E、F． （1）求证：四边形DEBF是平行四边形； （2）当DE＝DF时，求EF的长． 14．如图，AC＝8，分别以A、C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D．依次连接A、B、C、D，连接BD交AC于点O． （1）判断四边形ABCD的形状并说明理由； （2）求BD的长． 15．如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2． （1）求线段CE的长； （2）若点H为BC边的中点，连接HD，求证：HD＝HG． 16．如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M． （1）求证：△AHF为等腰直角三角形． （2）若AB＝3，EC＝5，求EM的长． 17．如图，矩形ABCD中，AB＝4，BC＝2，点E、F分别在AB、CD上，且BE＝DF＝． （1）求证：四边形AECF是菱形； （2）求线段EF的长． 18．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上． （1）求证：BG＝ ... ...