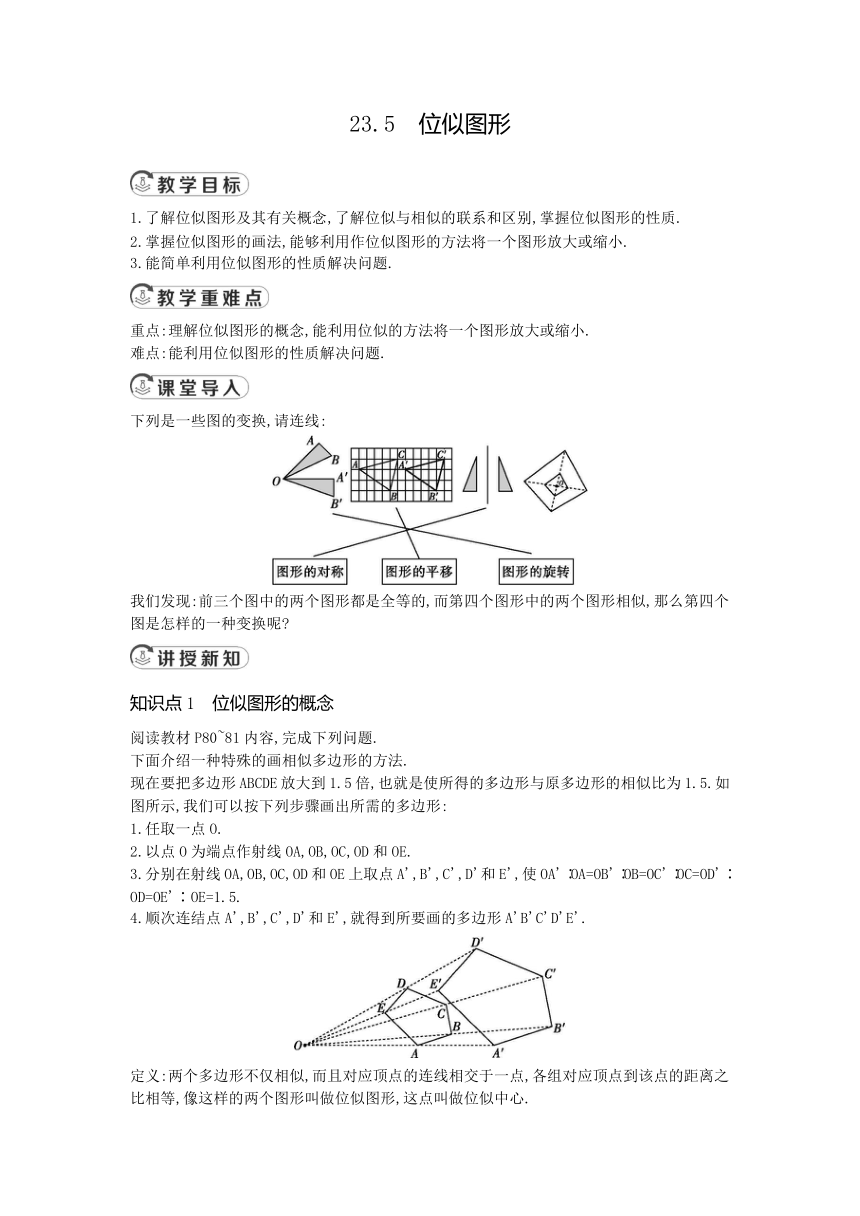
23.5 位似图形 1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质. 2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小. 3.能简单利用位似图形的性质解决问题. 重点:理解位似图形的概念,能利用位似的方法将一个图形放大或缩小. 难点:能利用位似图形的性质解决问题. 下列是一些图的变换,请连线: 我们发现:前三个图中的两个图形都是全等的,而第四个图形中的两个图形相似,那么第四个图是怎样的一种变换呢 知识点1 位似图形的概念 阅读教材P80~81内容,完成下列问题. 下面介绍一种特殊的画相似多边形的方法. 现在要把多边形ABCDE放大到1.5倍,也就是使所得的多边形与原多边形的相似比为1.5.如图所示,我们可以按下列步骤画出所需的多边形: 1.任取一点O. 2.以点O为端点作射线OA,OB,OC,OD和OE. 3.分别在射线OA,OB,OC,OD和OE上取点A',B',C',D'和E',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=OE'∶OE=1.5. 4.顺次连结点A',B',C',D'和E',就得到所要画的多边形A'B'C'D'E'. 定义:两个多边形不仅相似,而且对应顶点的连线相交于一点,各组对应顶点到该点的距离之比相等,像这样的两个图形叫做位似图形,这点叫做位似中心. [归纳] 1.如上图,五边形ABCDE∽五边形A'B'C'D'E',这两个图形对应顶点的连线相交于点O,所以这两个图形是位似图形,点O是位似中心. 2.位似图形的性质: (1)位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等; (2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比); (3)对应线段平行或者在一条直线上. 范例应用 例1 判断如图所示的各图中的两个图形是否是位似图形,如果是,请指出其位似中心. 解:(1)是位似图形,位似中心为点A. (2)是位似图形,位似中心为点P. (3)不是位似图形. (4)是位似图形,位似中心为点O. (5)不是位似图形. [方法归纳] (1)判断两个图形是不是位似图形的关键:①两个图形是相似图形;②两个相似图形的每组对应点的连线都经过同一点(位似中心).二者缺一不可; (2)找位似中心的方法:连结两组对应点连线的交点就是位似中心. 知识点2 位似图形的画法 范例应用 例2 如图所示,已知△DEF和△ABC位似,且相似比为2,位似中心为点O,请画出△DEF. 解:法一 如图所示,画射线OA,OB,OC; 在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC. 顺次连结D,E,F,则△DEF与△ABC位似,相似比为2. 还有其他画法吗 法二 △ABC与△DEF异侧 解:画射线AO,BO,CO;在射线AO,BO,CO上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC; 顺序连结D,E,F,则△DEF与△ABC位似,相似比为2. [方法归纳] (1)利用位似变化可以把一个图形放大或缩小. 比如画四边形ABCD的位似图形: 任取一点O,作直线OA,OB,OC,OD,在点O的另一侧取点A',B',C',D',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=2, 这样就可以得到放大到2倍的四边形A'B'C'D'. 实际上,如图所示,如果把位似中心取在多边形内,那么也可以把一个多边形放大或缩小,而且比较简便. (2)作位似变换的步骤: ①确定位似中心; ②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点; ③确定相似比,根据相似比的取值,可以判断是将一个图形放大还是缩小; ④找到对应点,顺次连结,即可得到位似变换后的图形. (3)符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形. 1.如图所示的两个四边形是位似图形,它们的位似中心是(D) A.点M B.点N C.点O D.点P 2.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直 ... ...
~~ 您好,已阅读到文档的结尾了 ~~