17.2 直角三角形 同步练（含答案） 2025-2026学年数学冀教版（2024）八年级上册

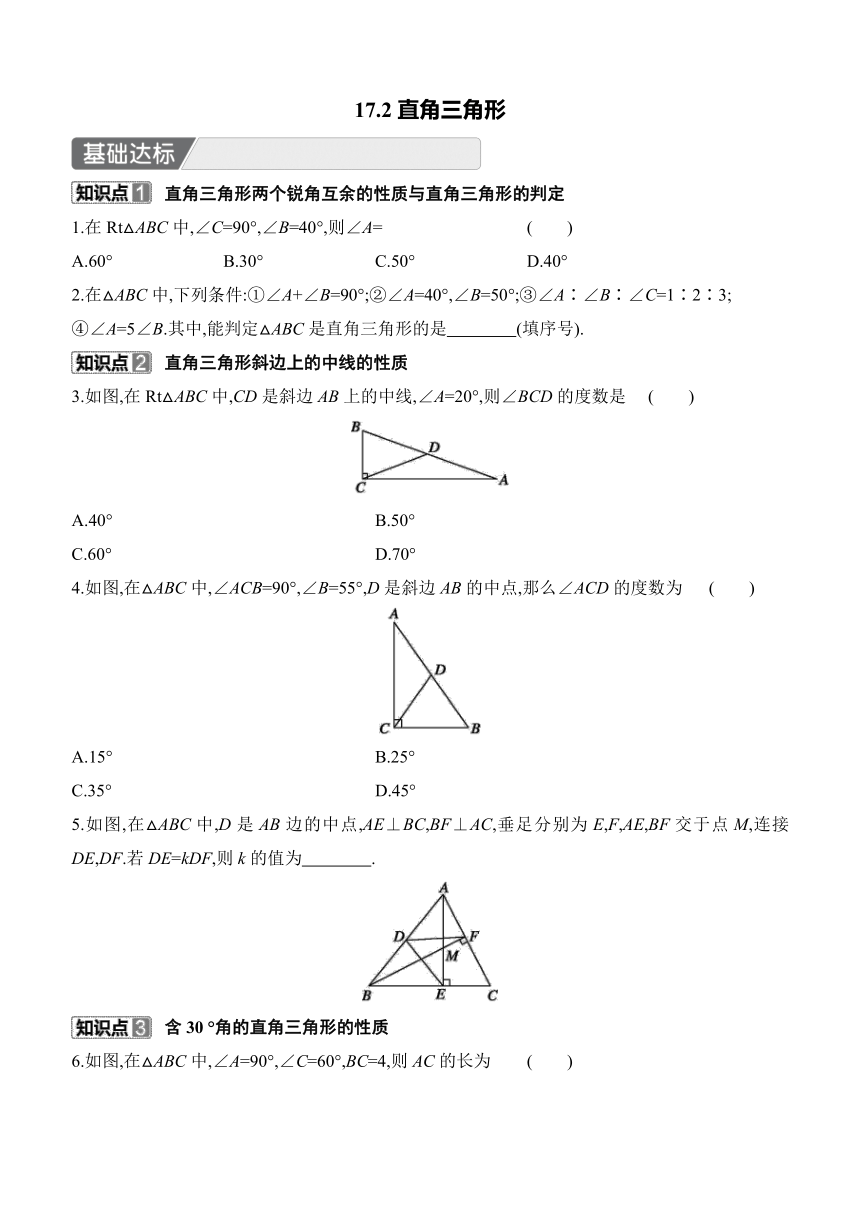
17.2直角三角形 直角三角形两个锐角互余的性质与直角三角形的判定 1.在Rt△ABC中,∠C=90°,∠B=40°,则∠A= (　　) A.60° B.30° C.50° D.40° 2.在△ABC中,下列条件:①∠A+∠B=90°;②∠A=40°,∠B=50°;③∠A∶∠B∶∠C=1∶2∶3; ④∠A=5∠B.其中,能判定△ABC是直角三角形的是　　　　(填序号). 直角三角形斜边上的中线的性质 3.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD的度数是 (　　) A.40° B.50° C.60° D.70° 4.如图,在△ABC中,∠ACB=90°,∠B=55°,D是斜边AB的中点,那么∠ACD的度数为 (　　) A.15° B.25° C.35° D.45° 5.如图,在△ABC中,D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为　　　　. 含30 °角的直角三角形的性质 6.如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为 (　　) A.1 B.1.5 C.2 D.2.5 1.(名师原创)如图,在△ABC中,∠A=∠B=∠C,D是AB的中点,连接CD,若CD=3,则AB的长为(　　) A.6 B.5 C.3 D.1.5 2.如图,一架梯子AB斜靠在竖直墙面上,点M为梯子AB的中点,当梯子底端向左水平滑动到点D位置时,滑动过程中OM的变化规律是 (　　) A.变小 B.不变 C.变大 D.先变小再变大 3.如图,在△ABC中,∠A=40°,∠C=90°,线段AB的垂直平分线交AB于点D,交AC于点E,则∠EBC=　　　　. 4.如图,它是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4 m,∠A=30°.求DE的长和∠BCD的度数. 5.如图,在△ABC中,AD是中线,∠ABC=∠ACB,CE⊥AB于点E,交AD于点O,F是AC的中点,连接EF,DE,DF. (1)若∠B=67°,求∠BAD的度数. (2)求证:直线DF垂直平分CE. (3)若∠BAC=45°,AO=a,AB=b,直接写出△DEF的周长(用含有a,b的代数式表示). 微专题7 构造含30°角的直角三角形的常用技巧 　　 含30°角的直角三角形是一个重要的数学模型,常用于线段的计算或证明一条线段是另一条线段的2倍,所以当图中没有含30°角的直角三角形时,常通过作辅助线构造该图形,而作辅助线的技巧主要是连接、作垂线或延长等. 1.如图,在△ABC中,AB=AC,∠C=30°,点D是AB的中点,过点D作DE⊥AB交BC于点E,DE=2,则CE的长度为 (　　) A.7 B.8 C.9 D.10 2.小亮想测量某池塘的宽度,他结合所学的数学知识并考虑到地形条件,设计了如图所示的测量方案:先在池塘外的空地上任取一点O,连接AO,CO,并延长CO至点D,使OC= OD,过点D作AC的平行线DE,延长AO至点F,连接EF,测得∠DEF=120°,∠OFE=90°,DE= 5 m,EF=9 m,请求出池塘宽度AC. 【详解答案】 基础达标 1.C　2.①②③　3.D　4.C　5.1 6.C 能力提升 1.A　解析:∵∠B=∠A,∠C=∠A,∠A+∠B+∠C=180°,∴∠A+∠A+∠A=180°,解得∠A=50°,∴∠B=40°, ∴△ABC是直角三角形,且AB是斜边,∵D是AB的中点,∴AB=2CD=2×3=6.故选A. 2.B　解析:∵∠AOB=90°,M为AB的中点,∴OM=AB.同理,OM=CD.∵AB=CD,∴OM的长度不变.故选B. 3.10°　解析:∵∠C=90°,∠A=40°,∴∠ABC=90°-∠A=50°.∵DE是线段AB的垂直平分线,∴AE=BE. ∴∠EBA=∠A=40°.∴∠EBC=∠ABC-∠EBA=50°-40°=10°. 4.解:∵DE⊥AC,BC⊥AC,∠A=30°, ∴BC=AB=BD=×7.4=3.7(m). 又AD=AB=3.7 m, ∴DE=AD=1.85 m. 在Rt△ACB中,∠ABC=60°, 又BC=BD, ∴△BCD是等边三角形, ∴∠BCD=60°. 答:立柱DE的长是1.85 m.∠BCD=60°. 5.解:(1)∵∠ABC=∠ACB, ∴AB=AC. ∵AD是△ABC的中线, ∴AD⊥BC. ∴∠B+∠BAD=90°. ∵∠B=67°, ∴∠BAD=90°-67°=23°. (2)证明:∵F是AC的中点, ∴CF=AC. ∵CE⊥AB, ∴∠AEC=∠BEC=90°. ∴EF=AC. ∴EF=CF. ∴点F在CE的垂直平分线上. ∵D是BC的中点, ∴CD=ED=BC. ∴点D在CE的垂直平分线上. ∴直线DF垂直平分CE. (3)△DEF的周长为a+b. 解析:∵∠AEC=90°,∠BAC=45°,AC=AB=b,F是AC的中点, ∴EF ... ...