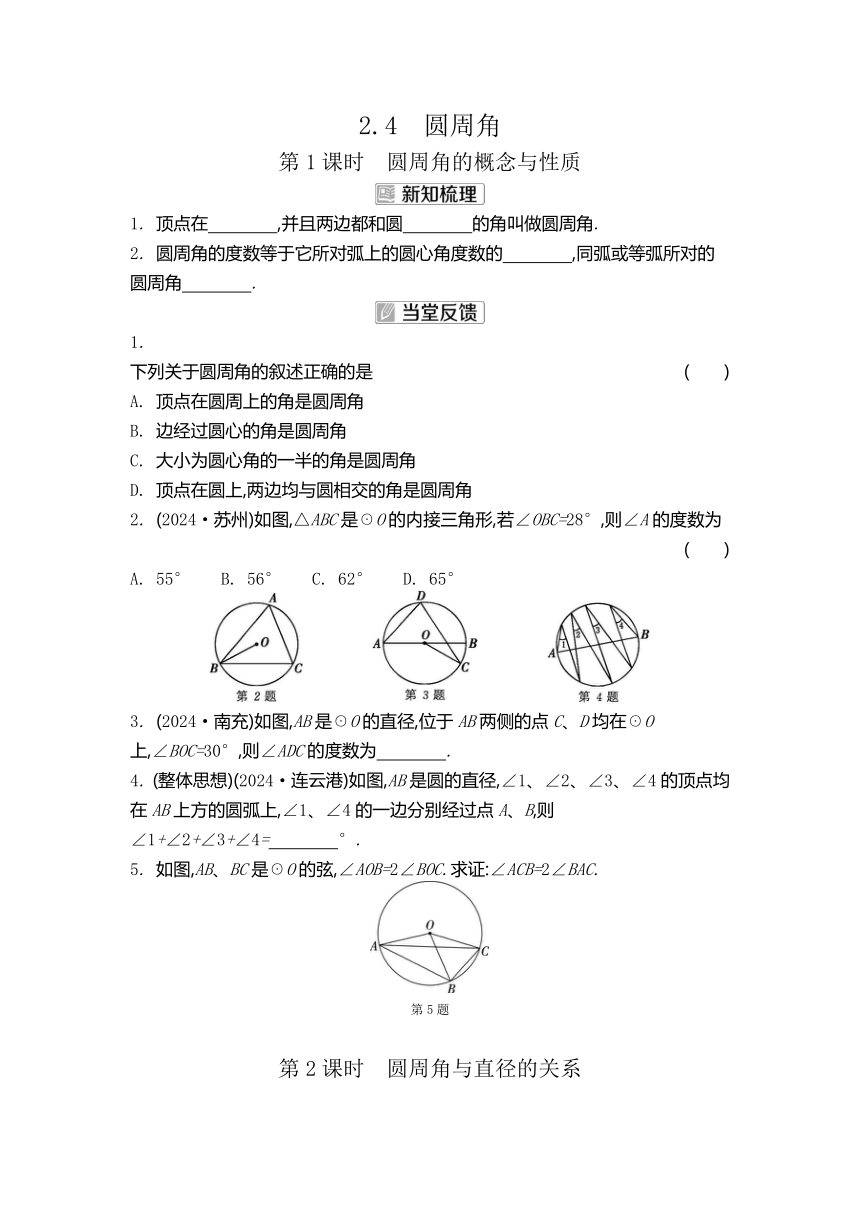
2.4 圆周角 第1课时 圆周角的概念与性质 1. 顶点在 ,并且两边都和圆 的角叫做圆周角. 2. 圆周角的度数等于它所对弧上的圆心角度数的 ,同弧或等弧所对的圆周角 . 1. 下列关于圆周角的叙述正确的是 ( ) A. 顶点在圆周上的角是圆周角 B. 边经过圆心的角是圆周角 C. 大小为圆心角的一半的角是圆周角 D. 顶点在圆上,两边均与圆相交的角是圆周角 2. (2024·苏州)如图,△ABC是☉O的内接三角形,若∠OBC=28°,则∠A的度数为 ( ) A. 55° B. 56° C. 62° D. 65° 3. (2024·南充)如图,AB是☉O的直径,位于AB两侧的点C、D均在☉O上,∠BOC=30°,则∠ADC的度数为 . 4. (整体思想)(2024·连云港)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4= °. 5. 如图,AB、BC是☉O的弦,∠AOB=2∠BOC.求证:∠ACB=2∠BAC. 第5题 第2课时 圆周角与直径的关系 所对的圆周角是直角,90°的圆周角所对的弦是 . 1. (2023·珠海)如图,AB是☉O的直径,BC是☉O的弦,∠BAC=50°,则∠D的度数为 ( ) A. 20° B. 40° C. 50° D. 80° 2. 如图,△ABC的边AB是☉O的直径,D是BC的中点,则△ABC一定是 ( ) A. 直角三角形 B. 钝角三角形 C. 等腰三角形 D. 等边三角形 3. (2024·常州)如图,AB是☉O的直径,CD是☉O的弦,连接AD、BC、BD.若∠BCD=20°,则∠ABD= °. 4. 如图,点A、B、C、D在☉O上,AC⊥BC,AC=4,∠ADC=30°,则BC的长为 . 5. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,连接BD. (1) 求证:DE=DB; (2) 若∠BAC=90°,BD=4,求△ABC外接圆的半径. 第5题 第3课时 圆的内接四边形 1. 一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆的 ,这个圆叫做四边形的 . 2. 圆内接四边形的性质定理:圆内接四边形的对角 . 1. (2024·苏州高新区二模)如图,四边形ABCD内接于☉O,P为边AD上任意一点(点P不与点A、D重合),连接CP.若∠B=120°,则∠APC的度数可能为 ( ) A. 30° B. 45° C. 50° D. 65° 2. (2024·牡丹江)如图,四边形ABCD是☉O的内接四边形,AB是☉O的直径.若∠BEC=20°,则∠ADC的度数为 ( ) A. 100° B. 110° C. 120° D. 130° 3. 如图,在圆内接四边形ABCD中,∠A∶∠B∶∠C=4∶3∶5,则∠D的度数是 . 4. (2024·广元)如图,四边形ABCD是☉O的内接四边形,E为AD延长线上一点,∠AOC=128°,则∠CDE= °. 5. 如图,四边形ABCD内接于☉O,AD是☉O的直径,C是的中点,AB、DC的延长线交于☉O外一点E.求证:BC=EC. 第5题 2.4 圆 周 角 第1课时 圆周角的概念与性质 1. 圆上 相交 2. 一半 相等 1. D 2. C 3. 75° 4. 90 5. ∵ ∠BAC=∠BOC,∠ACB=∠AOB,∠AOB=2∠BOC,∴ ∠ACB=×2∠BOC=∠BOC=2∠BAC,即∠ACB=2∠BAC 第2课时 圆周角与直径的关系 直径 直径 1. B 2. C 3. 70 4. 4 5. (1) ∵ AD平分∠BAC,BE平分∠ABC,∴ ∠BAE=∠CAD,∠ABE=∠CBE.∵ =,∴ ∠DBC=∠CAD,∴ ∠DBC=∠BAE.∵ ∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴ ∠DBE=∠DEB,∴ DE=DB (2) 连接CD.∵ AD平分∠BAC,∴ 易得=,∴ CD=BD=4.∵ ∠BAC=90°,∴ BC是该外接圆的直径,∴ ∠BDC=90°,∴ 在Rt△BDC中,BC==4,∴ △ABC外接圆的半径=BC=×4=2 第3课时 圆的内接四边形 1. 内接四边形 外接圆 2. 互补 1. D 2. B 3. 120° 4. 64 5. 如图,连接AC.∵ AD是☉O的直径,∴ ∠ACD=∠ACE=90°.∵ 四边形ABCD内接于☉O,∴ ∠D+∠ABC=180°.∵ ∠ABC+∠EBC=180°,∴ ∠EBC=∠D.∵ C是的中点,∴ ... ...
~~ 您好,已阅读到文档的结尾了 ~~

