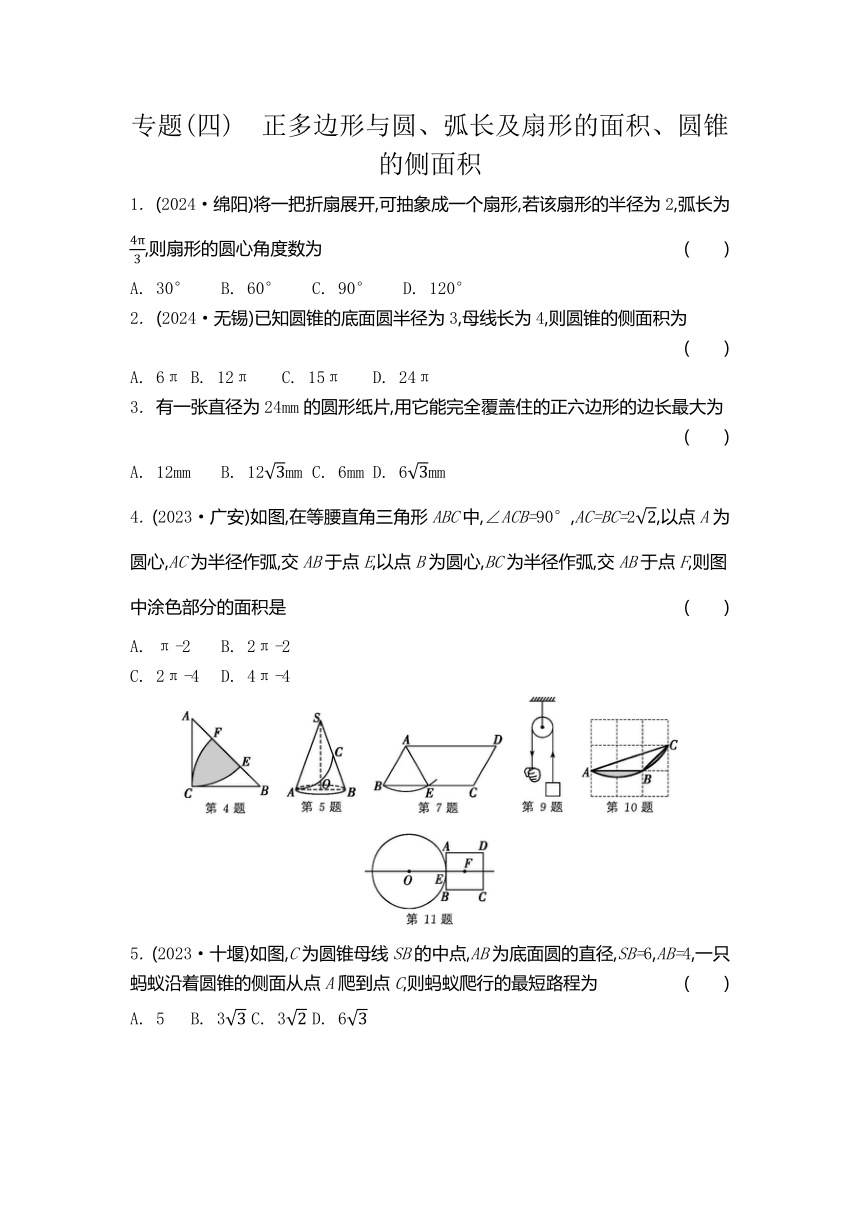
专题(四) 正多边形与圆、弧长及扇形的面积、圆锥的侧面积 1. (2024·绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角度数为 ( ) A. 30° B. 60° C. 90° D. 120° 2. (2024·无锡)已知圆锥的底面圆半径为3,母线长为4,则圆锥的侧面积为 ( ) A. 6π B. 12π C. 15π D. 24π 3. 有一张直径为24mm的圆形纸片,用它能完全覆盖住的正六边形的边长最大为 ( ) A. 12mm B. 12mm C. 6mm D. 6mm 4. (2023·广安)如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC为半径作弧,交AB于点E,以点B为圆心,BC为半径作弧,交AB于点F,则图中涂色部分的面积是 ( ) A. π-2 B. 2π-2 C. 2π-4 D. 4π-4 5. (2023·十堰)如图,C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从点A爬到点C,则蚂蚁爬行的最短路程为 ( ) A. 5 B. 3 C. 3 D. 6 6. (2024·德阳)已知正六边形ABCDEF的面积为6,则正六边形的边长为 . 7. (2024·镇江)如图,四边形ABCD为平行四边形,以点A为圆心,AB为半径画弧,交BC边于点E,连接AE.若AB=1,∠D=60°,则的长为 . 8. (2024·齐齐哈尔)若圆锥的底面圆半径是1cm,它的侧面展开图的圆心角是直角,则该圆锥的高为 cm. 9. (新考向·跨学科)(2024·昆山期末)如图,物理实验中利用一个半径为6cm的定滑轮提起砝码,小明向下拉动绳子一端,使得定滑轮逆时针转动了150°,此时砝码被提起了 cm. 10. (2023·仙桃)如图,在3×3的正方形网格中,每个小正方形的边长均为1,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点三角形ABC外接圆的一部分,则图中涂色部分的面积为 . 11. 如图,半径为2cm的☉O与边长为2cm的正方形ABCD的边AB相切于点E,点F为正方形ABCD的中心,直线OE过点F.当正方形ABCD沿直线OF以(2-)cm/s的速度向左运动 s时,☉O与正方形重叠部分的面积为cm2. 12. (2024·江西)如图,AB是半圆O的直径,D是弦AC的延长线上一点,连接BD、BC,∠D=∠ABC=60°. (1) 求证:BD是半圆O的切线; (2) 当BC=3时,求的长. 第12题 13. 如图,在☉O中,如果作两条互相垂直的直径AB、CD,那么弦AC是☉O的内接正方形的一边;以点A为圆心,OA为半径作弧,与☉O相交于点E、F,连接AE、BE、CE、EF.求证:弦AE、CE、EF分别是☉O的内接正六边形、正十二边形、正三角形的一边. 第13题 14. (2024·菏泽)如图,在四边形ABCD中,AD∥BC,∠DAB=60°,AB=BC=2AD=2.以点A为圆心,AD为半径作交AB于点E,以点B为圆心,BE为半径作交BC于点F,连接FD交于另一点G,连接CG. (1) 求证:CG为所在圆的切线; (2) 求图中涂色部分的面积. 第14题 专题(四) 正多边形与圆、弧长 及扇形的面积、圆锥的侧面积 1. D 2. B 3. A 4. C 5. B 6. 2 7. π 8. 9. 5π 10. 11. 1或(11+6) 12. (1) ∵ AB是半圆O的直径,∴ ∠ACB=90°,∴ 在Rt△ACB中,∠A+∠ABC=90°.∵ ∠D=∠ABC,∴ ∠D+∠A=90°,∴ 在△ABD中,∠ABD=90°.∵ AB是半圆O的直径,∴ BD是半圆O的切线 (2) 连接OC.∵ =,∠ABC=60°,∴ ∠AOC=2∠ABC=120°.∵ OC=OB,∠ABC=60°,∴ △BOC是等边三角形,∴ OC=BC=3,∴ 的长为=2π 13. 如图,连接OE、OF.∵ AB⊥CD,∴ ∠AOC=90°.∵ OA=AE=OE,∴ △AOE为等边三角形,∴ ∠AOE=60°,∴ =6,即弦AE是☉O的内接正六边形的一边.∵ ∠AOE=60°,∴ ∠EOC=90°-60°=30°,∴ =12,即弦CE是☉O的内接正十二边形的一边.∵ 易知∠AOF=60°,∴ ∠EOF=60°×2=120°,∴ =3,即弦EF是☉O的内接正三角形的一边 14. (1) 如图,连接BG.∵ AB=BC=2AD=2,∴ AD=AE=1,BE=BF=CF=1.∴ AD=BF.∵ AD∥BC,即AD∥BF,∴ 四边形ABFD是平行四边形,∴ ∠BFD=∠DAB=60°.∵ BG ... ...
~~ 您好,已阅读到文档的结尾了 ~~