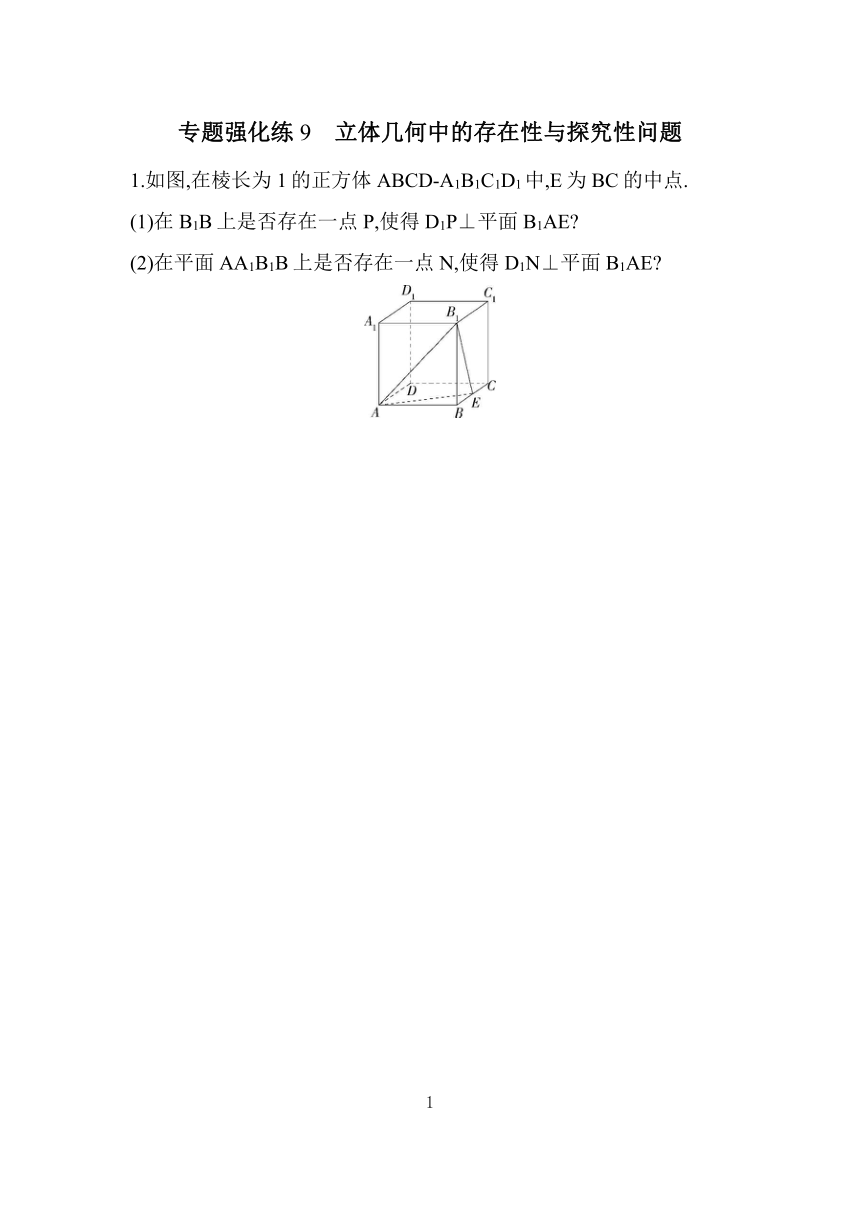
专题强化练9 立体几何中的存在性与探究性问题练习-《精讲精练》26版高中同步新教材数学北师大版（2019）选择性必修第一册

专题强化练9　立体几何中的存在性与探究性问题　　　　　 　　　　 　　　　 1.如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为BC的中点. (1)在B1B上是否存在一点P,使得D1P⊥平面B1AE (2)在平面AA1B1B上是否存在一点N,使得D1N⊥平面B1AE 如图①,在直角梯形ABCD中,AB∥CD,∠D=90°,四边形ABCE是边长为2的菱形,并且 ∠BCE=60°,以BE为折痕将△BCE折起,使点C到达C1的位置,且AC1=,如图②. (1)求证:平面BC1E⊥平面ABED; (2)在棱DC1上是否存在点P,使得点P到平面ABC1的距离为 若存在,求出直线EP与平面ABC1夹角的正弦值;若不存在,请说明理由. 3.已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2AB,△PAD是正三角形,CD⊥平面PAD,E,F,G,O分别是PC,PD,BC,AD的中点,连接PO,OG. (1)求平面EFG与平面ABCD的夹角; (2)在线段PA上是否存在点M,使得直线GM与平面EFG的夹角为 若存在,求出的值;若不存在,请说明理由. 4.如图,在直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M,N,Q分别为CC1,BC,AC的中点,点P在线段A1B1上运动,且=λ(λ∈[0,1]). (1)证明:无论λ取何值,总有AM⊥平面PNQ; (2)是否存在点P,使得平面PMN与平面ABC的夹角为60° 若存在,试确定点P的位置;若不存在,请说明理由. 答案与分层梯度式解析 专题强化练9　立体几何中的存在性与探究性问题1.解析　如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系, 则A(1,0,0),E,B1(1,1,1),D1(0,0,1), 所以. (1)假设在B1B上存在一点P,使得D1P⊥平面B1AE. 设P(1,1,z),则=(1,1,z-1), 所以无解, 故在B1B上不存在点P,使得D1P⊥平面B1AE. (2)假设在平面AA1B1B上存在点N,使得D1N⊥平面B1AE. 设N(1,b,c),则=(1,b,c-1), 所以 解得故N. 故在平面AA1B1B上存在点N,使得D1N⊥平面B1AE. 2.解析　(1)证明:如图①,连接AC,交BE于点O, ∵四边形ABCE是边长为2的菱形,∠BCE=60°,∴AC⊥BE,OA=OC=. 如图②,OA⊥BE,OC1⊥BE, ∴∠AOC1是二面角A-BE-C1的平面角, ∵AC1=, ∴OA⊥OC1,即∠AOC1=90°, ∴平面BC1E⊥平面ABED. 　 (2)存在.以O为坐标原点,OA,OB,OC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图②所示, 则D,0,0),B(0,1,0),E(0,-1,0), ∴ ,-1,0), 设,λ∈[0,1], 则, 设平面ABC1的一个法向量为n=(x,y,z), 则 令x=1,则y=,z=1,∴n=(1,,1), ∴点P到平面ABC1的距离d=,解得λ=或λ=(舍去), ∴, ∴, 设直线EP与平面ABC1的夹角为θ,θ∈, 则sin θ=|cos<,n>|=, ∴直线EP与平面ABC1夹角的正弦值为. 故在棱DC1上存在点P,使得点P到平面ABC1的距离为. 3.解析　(1)因为△PAD是正三角形,O为AD的中点,所以PO⊥AD. 因为CD⊥平面PAD,PO 平面PAD,所以PO⊥CD, 因为AD∩CD=D,所以PO⊥平面ABCD. 因为AD∥BC,AD=BC,O,G分别为AD,BC的中点,所以AO∥BG,AO=BG, 所以四边形ABGO为平行四边形,所以OG∥AB, 又AB⊥AD,所以OG⊥AD. 以O为坐标原点,OA,OG,OP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系, 设AB=2,则AD=4,A(2,0,0),G(0,2,0),P(0,0,2 ), 所以). 设平面EFG的一个法向量为n=(x,y,z), 则 取x=,可得n=(,0,1). 易知平面ABCD的一个法向量为m=(0,0,1), 所以cos=, 所以平面EFG与平面ABCD的夹角为. (2)假设在线段PA上存在点M,使得直线GM与平面EFG的夹角为, 设λ),0≤λ≤1, 则λ), 由题意可得|cos