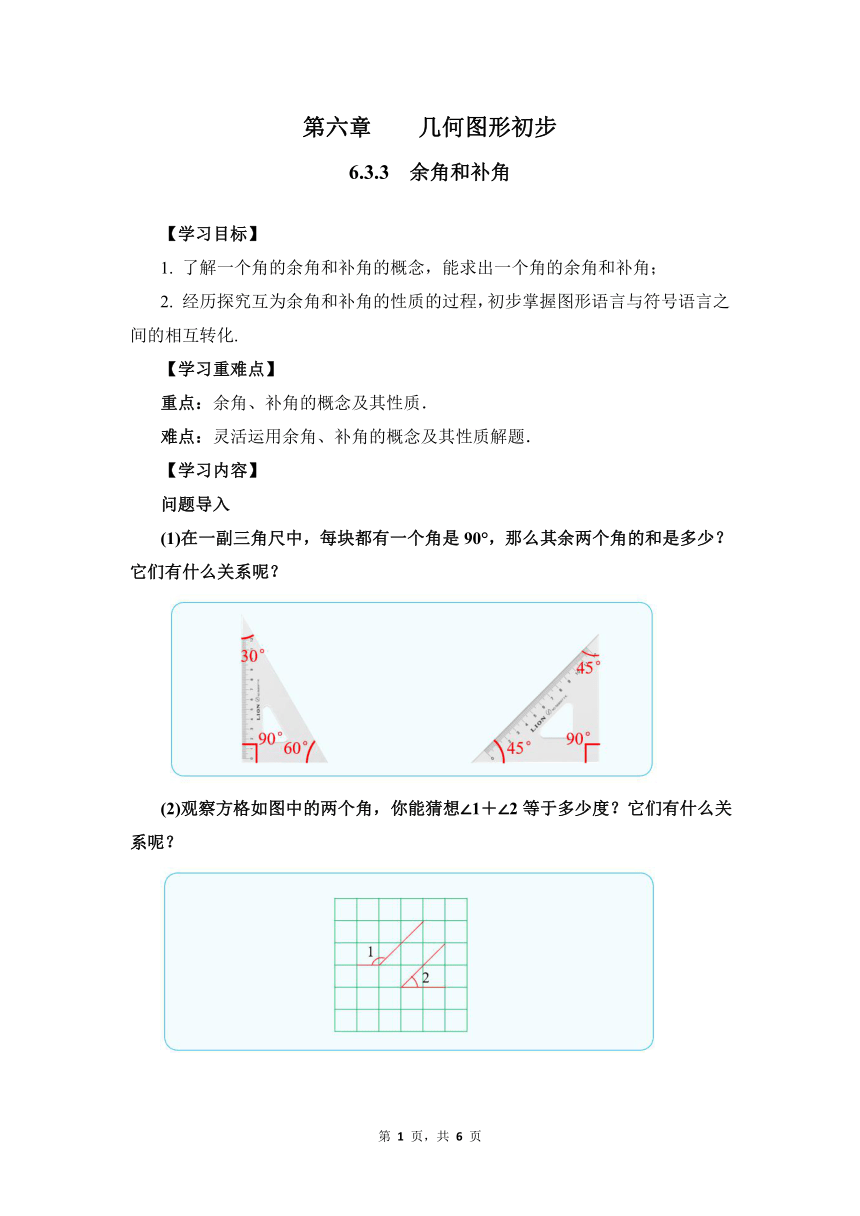
第六章 几何图形初步 6.3.3 余角和补角 【学习目标】 1. 了解一个角的余角和补角的概念,能求出一个角的余角和补角; 2. 经历探究互为余角和补角的性质的过程,初步掌握图形语言与符号语言之间的相互转化. 【学习重难点】 重点:余角、补角的概念及其性质. 难点:灵活运用余角、补角的概念及其性质解题. 【学习内容】 问题导入 (1)在一副三角尺中,每块都有一个角是90°,那么其余两个角的和是多少?它们有什么关系呢? (2)观察方格如图中的两个角,你能猜想∠1+∠2等于多少度?它们有什么关系呢? 新知探究 1.余角的概念 如果两个角的和等于_____,就说这两个角互为余角,简称互余,即其中的一个角是另外一个角的余角. 如果∠1=30°,∠2=60°,我们可以说∠1与∠2互余,或者可以说∠1是∠2的余角,还可以说_____. 图中给出的各角,哪些互为余角? 2.补角的概念 如果两个角的和等于_____,就说这两个角互为补角,简称互补,即其中的一个角是另外一个角的补角. 如果∠1=45°,∠2=135°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说_____. 图中给出的各角,哪些互为补角? 思考: ∠β=18°,余角= ,补角= . ∠β=35°,余角= ,补角= . ∠β=78°,余角= ,补角= . ∠β=63°,余角= ,补角= . 观察可得:锐角的补角比它的余角大 . 提醒: ①余角、补角都是成对出现的,单独的一个角、三个或三个以上的角之间不能说互余或互补; ②互余的两个角都必须是锐角,互补的两个角为一个锐角、一个钝角或两个角都是直角. 3.补角和余角的性质 思考: (1) 若∠1与∠2,∠3都互为余角,∠2与∠3的大小有什么关系? 因为∠1与∠2,∠3都互为余角, 所以∠2=90°-∠1,∠3=90°-∠1, 所以∠2=∠3. (2) 若∠1与∠2互余,∠3与∠4互余,且∠1=∠3,那么∠2与∠4的大小有什么关系? 因为∠1与∠2互余,∠3与∠4互余, 所以∠2=90°-∠1,∠4=90°-∠3, 因为∠1=∠3, 所以∠2=∠4. 由此,我们可以得到补角性质: _____ 类似地,余角的性质: _____ 巩固练习 1.若∠α=29°45′,则ㄥα的余角等于( ) A.60°55′ B.60°15′ C.150°55′ D.150°15′ 2.已知∠1与∠2互余,∠1=(7x-2)°,∠2=(3x+2)°,则x的值是 . 3.一个锐角的补角等于这个锐角的余角的3倍,求这个锐角的度数. 4. 已知∠α的余角是它补角的,求∠α的度数. 典例剖析 例3.如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,图中哪些角互为余角? 分析:为余角的两个角的和是90°,而已知条件中隐含互为补角的条件,再利用角平分线的条件,便可以发现互为余角的角. 解:∵A,O,B在同一直线上,∴∠AOC和∠BOC互为补角, 又∵射线OD和射线OE分别平分∠AOC和∠BOC, ∴∠COD+∠COE= ∠AOC+ ∠BOC =90 ° ∴∠COD和∠COE互为余角, 同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角. 巩固练习 1.已知∠1与∠2互补,∠3与∠4互补,且∠1=∠3,那么( ) A. ∠2> ∠4 B. ∠2< ∠4 C.∠2= ∠4 D. ∠2与∠4的大小不确定 2.如图,将一副三角板叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角板,则与∠AOD始终相等的角是( ) A.∠BOD B.∠ABO C. ∠BOC D. ∠BAO 3.如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角? 课堂练习 1.图中给出的各角中,哪些互为余角?哪些互为补角? 互为余角: . 互为补角: . 2. 一个角是70°39′,求它的余角和补角. 3. ∠α的补角是它的3倍,∠α是多少度? 4. 如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进入围墙,如何测量? 随堂检测 1.下列四个角中,最有可能与70°角互补的是( ) 2.下列图形中,∠1和∠2互为余角的是( ) 3.已 ... ...
~~ 您好,已阅读到文档的结尾了 ~~