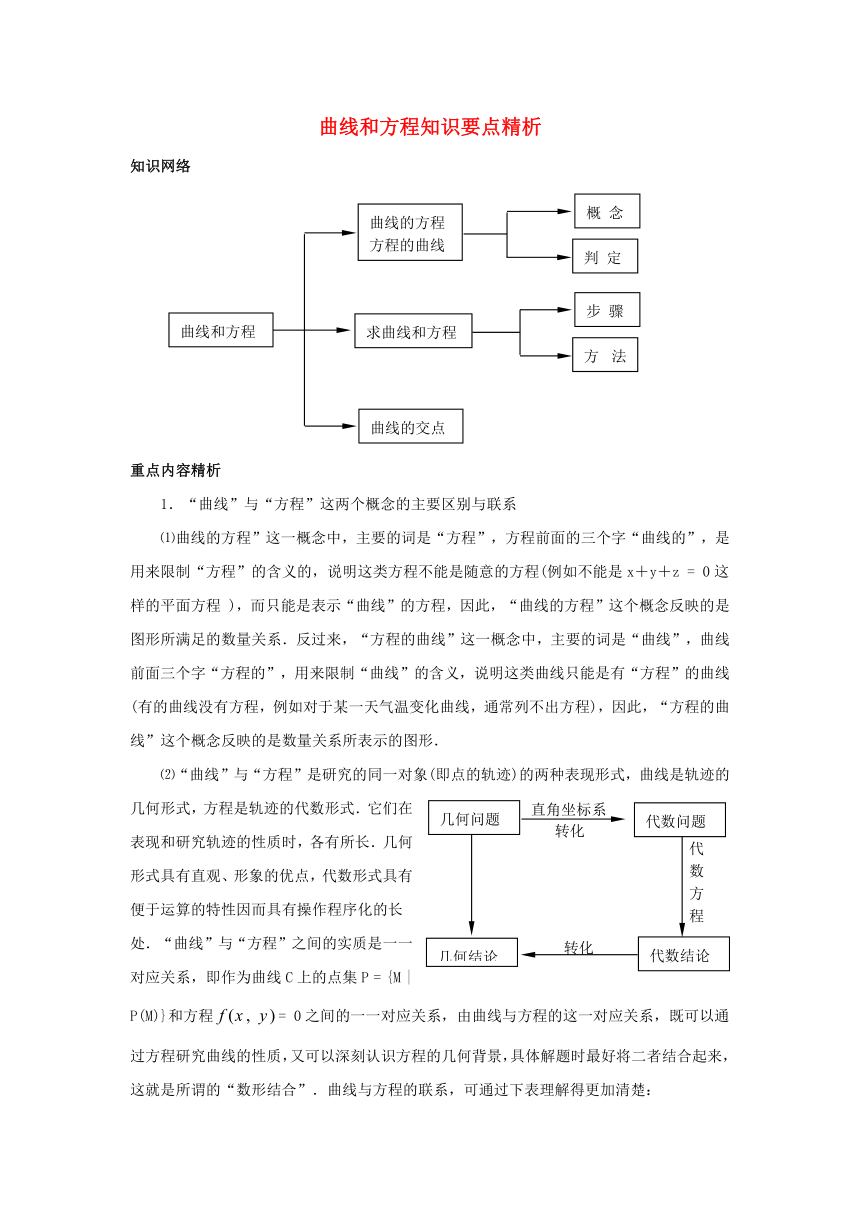
曲线和方程知识要点精析 知识网络 重点内容精析 1.“曲线”与“方程”这两个概念的主要区别与联系 ⑴曲线的方程”这一概念中,主要的词是“方程”,方程前面的三个字“曲线的”,是用来限制“方程”的含义的,说明这类方程不能是随意的方程(例如不能是x+y+z = 0这样的平面方程 ),而只能是表示“曲线”的方程,因此,“曲线的方程”这个概念反映的是图形所满足的数量关系.反过来,“方程的曲线”这一概念中,主要的词是“曲线”,曲线前面三个字“方程的”,用来限制“曲线”的含义,说明这类曲线只能是有“方程”的曲线(有的曲线没有方程,例如对于某一天气温变化曲线,通常列不出方程),因此,“方程的曲线”这个概念反映的是数量关系所表示的图形. ⑵“曲线”与“方程”是研究的同一对象(即点的轨迹)的两种表现形式,曲线是轨迹的几何形式,方程是轨迹的代数形式.它们在表现和研究轨迹的性质时,各有所长.几何形式具有直观、形象的优点,代数形式具有便于运算的特性因而具有操作程序化的长处.“曲线”与“方程”之间的实质是一一对应关系,即作为曲线C上的点集P = {M | P(M)}和方程= 0之间的一一对应关系,由曲线与方程的这一对应关系,既可以通过方程研究曲线的性质,又可以深刻认识方程的几何背景,具体解题时最好将二者结合起来,这就是所谓的“数形结合”.曲线与方程的联系,可通过下表理解得更加清楚: ⑶“曲线和方程”的定义中所列的两个条件,正好组成两个集合相等的充要条件,二者缺一不可,它是判断方程= 0是不是曲线C的方程的依据.例如,方程y = x不能叫做到两坐标轴距离相等的轨迹的方程,到两坐标轴距离相等的轨迹(曲线)也不能叫做方程y = x的曲线.用集合观点解释“曲线和方程”的定义:设P = {具有某种性质(或适合某种条件)的点},Q = {(x,y)|= 0},若M(x,y)有:①MP(x,y)Q,即PQ时;② (x,y)Q MP,即QP时,当且仅当PQ且QP,即P = Q时,才称方程= 0为曲线C的方程;曲线C为方程= 0的曲线(图形). 2.建立坐标系所遵循的一般原则 坐标系建立适当,可使运算过程简单,所得的方程也比较简单,否则会大大增加运算的繁难程度.在实际解题过程中,应充分利用图形的几何特性.如中心对称图形,可利用它的对称中心作为坐标原点;轴对称图形,可以利用它的对称轴作为坐标轴,使横、纵坐标互为相反数;条件中若有直角,可考虑两直角边作为坐标轴等等;原点取在某一定点,坐标轴选在某定直线段所在直线或图形的对称轴;设出各点的坐标,使用字母要尽可能的少. 3.求曲线方程的步骤 求曲线方程,一般有五个步骤,这五个步骤和列方程解应用题的步骤完全类似. ⑴依据已知几何条件建立适当的直角坐标系,用(x,y)表示曲线上任意一点M的坐标; ⑵列出适合条件p的点M的集合P = {M | P(M)};(此步根据情况可以省略) ⑶用坐标表示条件P(M),列出方程= 0; ⑷化方程= 0为最简形式; ⑸证明化简后的方程为所求曲线的方程,即验证以⑷中方程的解为坐标的点都在曲线上. 简记为建系、列式、代换、化简、证明. 这五步构成一个整体,每一步都有其特点和重要性.第一步在具体问题中有两种情况:⑴题设中给定坐标系;⑵题设中没有确定坐标系,必须选取适当的坐标系;第二步应仔细分析曲线的特征,注意揭示隐含条件,抓住与曲线上任意一点M有关的等量关系,列出几何等式;第三步在将几何条件转化为代数方程的过程中 ,常用到一些基本公式;第四步在化简过程中,注意运算的合理性与准确性,尽量避免“丢解”和“增根”;对第五步“证明”,从理论上讲是必要的,但实际处理上常被省略掉.如遇到特殊情况可适当予以说明,例如据审查,某些点虽然其坐标适合方程,但不在曲线上,那么可通过限制方程中x,y的取值范围予以剔除 ... ...
~~ 您好,已阅读到文档的结尾了 ~~