古埃及的数学 学案 (2)

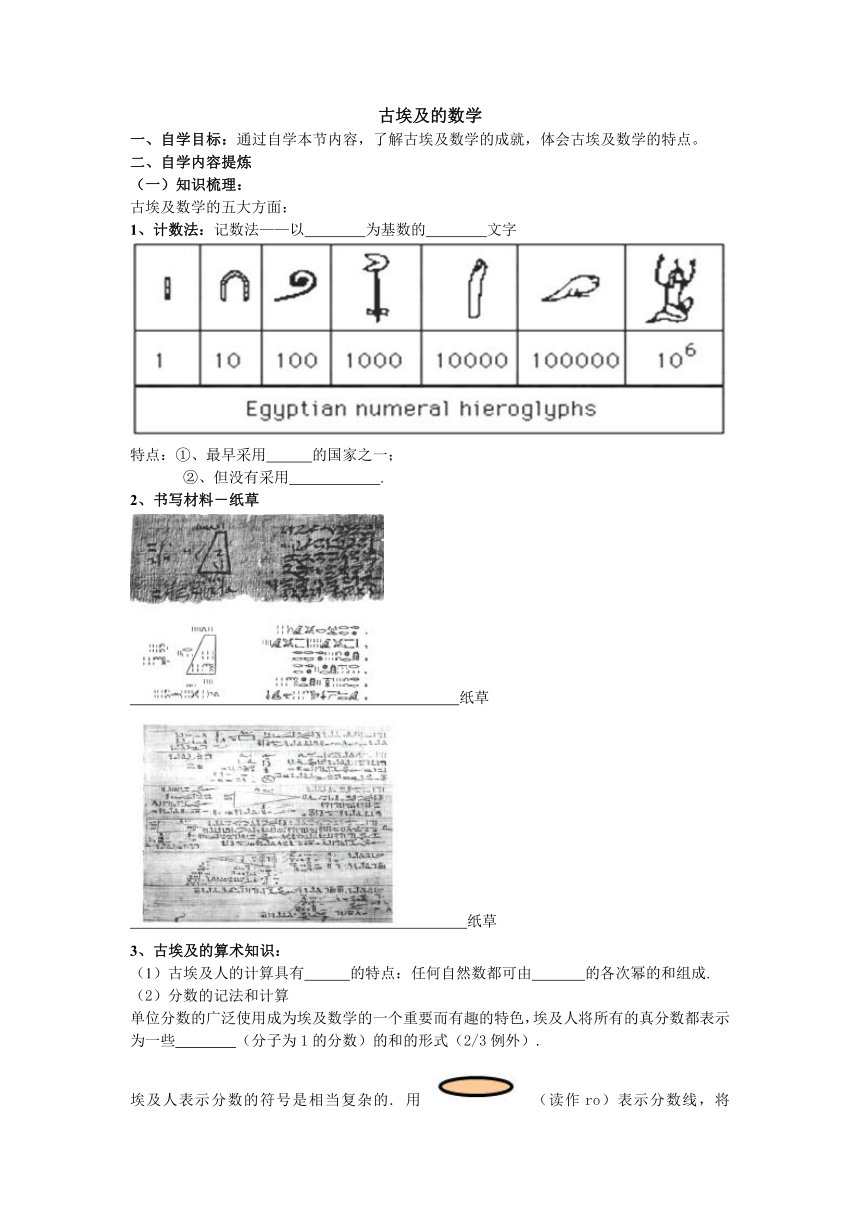
古埃及的数学 一、自学目标：通过自学本节内容，了解古埃及数学的成就，体会古埃及数学的特点。 二、自学内容提炼 （一）知识梳理： 古埃及数学的五大方面： 1、计数法：记数法———以 为基数的 文字 特点：①、最早采用 的国家之一； ②、但没有采用 . 2、书写材料－纸草 纸草 纸草 3、古埃及的算术知识： （1）古埃及人的计算具有 的特点：任何自然数都可由 的各次幂的和组成. （2）分数的记法和计算 单位分数的广泛使用成为埃及数学的一个重要而有趣的特色，埃及人将所有的真分数都表示为一些 （分子为1的分数）的和的形式（2/3例外）. 埃及人表示分数的符号是相当复杂的. 用（读作ro）表示分数线，将或点的记号放在数的上方用来表示分数.例如： （3）、完成了基本的算术四则运算 （4）、已经有了求近似平方根的方法 4、古埃及的代数： ①、有渐进的代数，但叙述方式是 ，很少引用符号； ②、比例的概念也已有萌芽；三角函数观念的萌芽 ③、一元一次方程求解 即形如：或某些二次方程： ④、等差级数和等比级数的概念及其求和 例1、兰德纸草书中有一方程问题：有一数量，它的2/3加它的1/2，加它的1/7，再加全部共为33. 用现代的记号是： 只不过分数部分写为 28/97=1/4+1/97+1/56+1/679+1/776+1/194+1/388. 古埃及人把未知数称为“堆”（aha) 例2、兰德纸草书中的第24题：已知“堆”与七分之一“堆”相加为19，求“堆”的值. “假位法”（method of false position）—先假设一个特殊的数作为“堆”的值（多半是假值），将其代入等式左边去运算，然后比较得数与应得的结果，再通过比例的方法算出正确的答案. 在上例中，用数7作为未知数x的实验值，于是有，左边= 而应得的结果是19，这两个结果之比为19/8=2+1/4+1/8，将7乘以（2+1/4+1/18）即得正确的“堆”值为16+1/2+1/8. 例3、几何级数（等比级数）.兰德纸草书第79题：是在数字 7，49，343，2401，16807 旁边各注有图人，猫，鼠，大麦，量器等字样，而且给出总数为19607. 问这个题目产生的是什么数列？总数是多少？--有答案无解法. 5、古埃及的几何： 在兰德纸草书和莫斯科纸草书中确实包含有许多几何性质的问题，内容大都与土地面积和谷堆体积的计算有关. 由此可知，古埃及的几何很发达. 几何问题多是讲度量法，涉及到田地的面积，谷仓的容积和有关金字塔的计算等. 著名的“金字塔之迷”就是其中的代表. （1）、法老胡夫的金字塔(Pyramid)： 兴建于齐阿斯王朝（BC2900年左右），高146.5米，塔基宽 233米，底边长度的误差为1.6厘米，正方程度与水平程度的平均误差≤1/10000，塔高与塔基之比非常近似于圆的周长与其半径之比.用以砌塔的巨石达230万块，重量从2.5吨到50吨不等.如把这些石头凿成平均一立方英尺的小块并排列成行，其长度相当于地球周长的2/3. 10万人用了20年的时间才建成的. （2）、阿蒙神庙(Oman Tamples)：阿蒙———埃及的太阳神.王殿总面积5000平方米，有134根圆柱，中间最高的12根高达21米. ①、正方形,矩形,三角形,梯形面积公式.其他几何图形近似计算. 如：任意四边形的面积 ②、已经知道毕达哥拉斯定理的特殊情况. ③、圆的面积很好的近似. Rhind 50:假设一直径为9的圆形土地，其面积=边长为8的正方形土地. 由此可知，圆面积为 ，其中 d 为直径，相当于取π=3.1605，误差为0.6%. ④、体积的计算 正四棱台的体积－最高成就. 直棱柱(圆柱)的体积等于底面积乘以高. ⑤、半球表面积的计算公式. ⑥、知道相似三角形. ⑦、在求圆面积以及把圆分为若干相等部分的问题上，已经有了正确的知识. （二）典例选讲 1、迭加运算 例如： 计算 27×31 例：计算745÷26，只要连续地把除数26加倍，直到再加倍就超过745为止. 2、分数运算 2/5=1/3+1/15 2/7=1/4+1/28 2/9=1/6 ... ...